Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Beispiel: Quadratische Betragsungleichung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Die Betragsungleichung

$\displaystyle \vert 2x^2-3\vert\leq x+1 \,. $

wird zunächst graphisch gelöst.

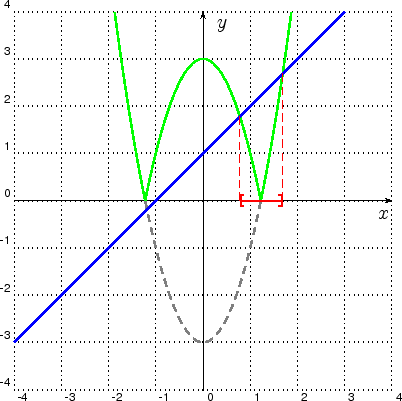
\includegraphics{bild07}

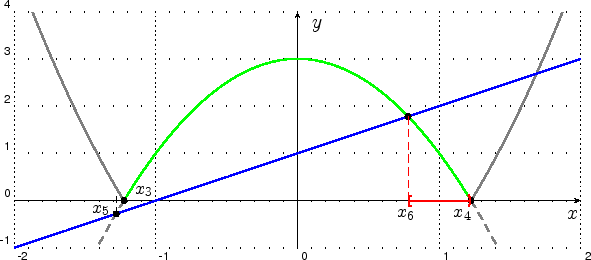
Die grau gestrichelte Kurve zeigt den Bereich von $ 2x^2-3$, der unterhalb der $ x$-Achse verläuft. Durch das bilden des Betrags wird dieser negative Teil nach oben gespiegelt. Die grüne Kurve zeigt also die linke Seite $ \vert 2x^2-3\vert$ der Ungleichung. Die blaue Kurve zeigt das Schaubild der rechten Seite $ x+1$. Lösungen der Ungleichung sind alle $ x$-Werte in denen die grüne Kurve unterhalb der blauen verläuft, sowie die $ x$-Werte für die sich die Schaubilder schneiden. Das Lösungsintervall ist rot eingezeichnet.

Für die rechnerische Lösung unterscheidet man zwei Fälle.

Fall 1: $ 2x^2-3 \geq 0$. Dann folgt

\begin{displaymath} \begin{array}{cccc} &\vert 2x^2-3\vert&\leq &x+1\\ [1mm] \Lo... ...& x+1\\ [1mm] \Longleftrightarrow&2x^2-x-4 &\leq& 0 \end{array}\end{displaymath}

Die Nullstellen der linken Seite, d.h. die $ x$-Werte für die $ 2x^2-3=x+1$ ist, sind

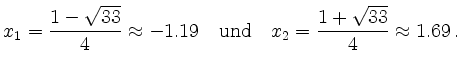
$\displaystyle x_1=\frac{1-\sqrt{33}}{4}\approx -1.19 \textrm{ \ \ und \ \ } x_2=\frac{1+\sqrt{33}}{4}\approx 1.69\,.$

Die Lösungen der Ungleichung im Fall 1 sind also die $ x$-Werte mit $ x_1 \leq x \leq x_2$ für die gleichzeitig noch $ 2x^2-3 \geq 0$ gilt. Die Nullstellen von $ 2x^2-3$ sind

$\displaystyle x_3=- \sqrt{3/2}\ \approx -1.22 \textrm{ \ \ und \ \ } x_4=\sqrt{3/2}\ \approx 1.22 \,.$

Damit ist $ 2x^2-3 \geq 0$ wenn $ x\leq x_3$ oder $ x \geq x_4$ gilt. Wegen

$\displaystyle x_3 < x_1 < x_4 < x_2 $

ist das Intervall $ {L}_1=[x_4,x_2]$ die Lösungsmenge im Fall 1.

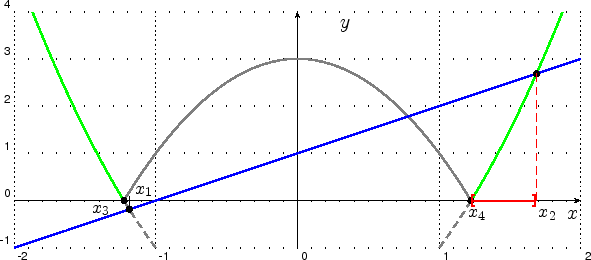
\includegraphics{bild08}

Fall 2: $ 2x^2-3 < 0$. Dann folgt

\begin{displaymath} \begin{array}{cccc} &\vert 2x^2-3\vert&\leq &x+1\\ [1mm] \Lo... ... x+1\\ [1mm] \Longleftrightarrow&-2x^2-x+2 &\leq& 0 \end{array}\end{displaymath}

Die Nullstellen der linken Seite sind

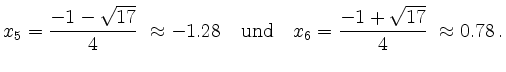
$\displaystyle x_5=\frac{-1-\sqrt{17}}{4} \ \approx -1.28 \textrm{ \ \ und \ \ } x_6=\frac{-1+\sqrt{17}}{4}\ \approx 0.78\,.$

Die Lösungen im zweiten Fall sind also die $ x$-Werte mit $ x\leq x_5$ oder $ x \geq x_6$ für die gleichzeitig $ 2x^2-3 < 0$, d.h. $ -2x^2+3 >0$ gilt. Dies ist für

$\displaystyle x_3=-\sqrt{3/2} \ <\ x\ < \ \sqrt{3/2}=x_4$

der Fall. Die Lösungsmenge im zweiten Fall ist also durch das Intervall $ {L}_2=[x_6,x_4)$ beschrieben.

\includegraphics{bild10}

Insgesamt ergibt sich als Lösungsmenge für die Ungleichung

$\displaystyle {L}={L}_1 \cup {L}_2=[x_4,x_2] \cup [x_6,x_4)=%[x_6,x_4) \cup [x_4,x_2] = [x_6,x_2] =\left[ \frac{-1+\sqrt{17}}{4},\frac{1+\sqrt{33}}{4} \right]\,.$

(Autor: Vorkurs Mathematik)

siehe auch:

  automatisch erstellt am 23. 10. 2007