Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Beispiel: Resultante bei Polynomen in zwei Variablen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Mit Hilfe von Resultanten können polynomiale Gleichungen in mehreren Variablen gelöst werden. Als Beispiel wird das System

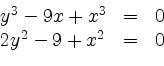
\begin{displaymath} \begin{array}{lll} y^3 - 9x + x^3 &=& 0 \\ 2y^2 - 9 + x^2 &=& 0 \end{array} \end{displaymath}

betrachtet. Man interpretiert die linken Seiten als Polynome in $ x$ mit von $ y$ abhängigen Koeffizienten $ a_k$ bzw. $ b_k$ der Monome $ x^k$:

$\displaystyle a_0=y^3,\,a_1=-9,\,a_2=0,\,a_3=1,\quad b_0=2y^2-9,\,b_1=0,\,b_2=1 \,. $

Die Gleichungen haben genau dann gemeinsame Lösungen, wenn die Resultante der beiden Polynome verschwindet:

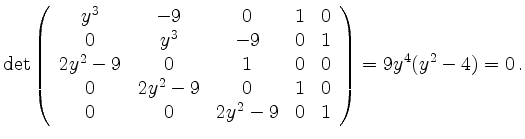
$\displaystyle \det \left(\begin{array}{ccccc} y^3 & -9 & 0 & 1 & 0 \\ 0 & y... ... 0 \\ 0 & 0 & 2 y^2-9 & 0 & 1 \end{array}\right) = 9 y^4(y^2-4) =0 \,. $

Die möglichen $ y$-Werte $ 0,\pm 2$ setzt man nun in das polynomiale System ein und kann so die zugehörigen $ x$-Werte bestimmen. Dabei ist zu beachten, dass für eine Nullstelle $ y$ die Nullstellenmengen (bezüglich $ x$) der beiden Polynome nicht übereinstimmen müssen. Der Durchschnitt beider Mengen liefert jeweils die Lösungen des Systems.

Aus der zweiten Gleichung erhält man

Durch Einsetzen dieser Werte in die erste Gleichung sieht man dass

$\displaystyle (0,3)\,,\,(0,-3)\,,\,(2,1)\,,\,(-2,-1) $

Lösungen des Systems sind, nicht jedoch $ (2,-1)\,,\,(-1,2)$.

\includegraphics[width=.7\linewidth]{Bild_Bsp_Resultante2.eps}

Die Abbildung zeigt die Lösungsmenge als Schnittpunkte der beiden algebraischen Kurven.

(Autor: J. Koch)

siehe auch:

  automatisch erstellt am 7.  1. 2008