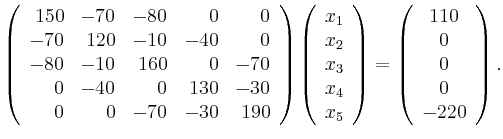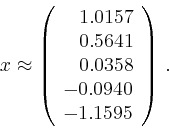Bezeichnet man in einem elektrischen Schaltkreis
mit 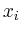 die Kreisströme mit Fließrichtung
entgegen dem Uhrzeigersinn, mit
die Kreisströme mit Fließrichtung
entgegen dem Uhrzeigersinn, mit 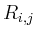 den
gemeinsamen Widerstand der
den
gemeinsamen Widerstand der 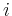 -ten und
-ten und
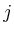 -ten Schleife und mit
-ten Schleife und mit
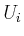 die angelegten Spannungen,
so ergibt sich aus dem Ohmschen und
dem Kirchhoffschen Gesetz das lineare Gleichungssystem
die angelegten Spannungen,
so ergibt sich aus dem Ohmschen und
dem Kirchhoffschen Gesetz das lineare Gleichungssystem
Dabei bedeutet 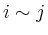 ,
dass die
,
dass die 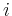 -te und
-te und 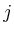 -te Schleife einen
gemeinsamen Widerstand haben.
-te Schleife einen
gemeinsamen Widerstand haben.
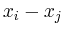 ist der Strom durch diesen
Widerstand.
Mit
ist der Strom durch diesen
Widerstand.
Mit 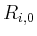 ,
, 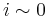 ,
werden Widerstände bezeichnet, die nur in der
,
werden Widerstände bezeichnet, die nur in der
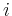 -ten Schleife liegen.
-ten Schleife liegen.
Beispielsweise erhält man für den abgebildeten
Schaltkreis das lineare Gleichungssystem
Die Koeffizientenmatrix
enthält in der
Diagonale jeweils die Summe
der zu einer Schleife gehörigen Widerstände und
in Position 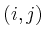 den negativen
gemeinsamen Widerstand der Schleifen
den negativen
gemeinsamen Widerstand der Schleifen 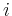 und
und 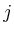 .
Die Lösung für das betrachtete Beispiel ist
.
Die Lösung für das betrachtete Beispiel ist
(Autoren: App/Höllig)
siehe auch:
| |
automatisch erstellt
am 23. 5. 2011 |




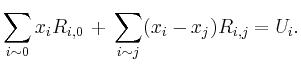
![\includegraphics[width=\moimagesize]{b_elektrischer_schaltkreis}](/inhalt/beispiel/beispiel4/img11.png)