Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Kurvendiskussion einer periodischen Funktion

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Es wird eine Funktionsuntersuchung für die Funktion

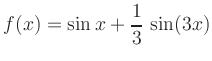
$\displaystyle f(x)=\sin x + \frac{1}{3}\,\sin(3x)$

durchgeführt.

Symmetrie: Da $ \sin x=-\sin(-x)$ ist die Funktion ungerade.

Periodizität: Die Funktion ist wie die Sinusfunktion selbst $ 2\pi$-periodisch und wird im Folgenden daher nur auf dem Intervall $ [-\pi,\pi]$ betrachtet.

Unstetigkeitsstellen und Polstellen: Die Funktion ist aus stetigen Funktionen zusammengesetzt und hat daher keine Unstetigkeitsstellen oder Polstellen.

Nullstellen: Aus dem Additionstheorem folgt $ \sin(3x) = 3\sin x -4\sin^3 x$, und somit ist

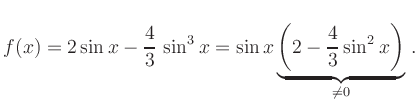
$\displaystyle f(x) = 2 \sin x -\frac{4}{3}\,\sin^3 x = \sin x \underbrace{\left(2-\frac{4}{3}\sin^2 x \right)}_{\neq 0} \,. $

Die Funktion besitzt also Nullstellen bei 0 und $ \pm \pi$.

Extrema: Die Ableitung

$\displaystyle f^\prime(x) = 2 \cos x -4\sin^2 x \,\cos x =-2\cos x +4\cos^3 x $

ist Null für $ \cos x =0$ oder $ \cos x =\pm 1/\sqrt{2}$, also

$\displaystyle x=\pm \pi/2 \quad\lor\quad x=\pm \pi/4 \quad\lor\quad x= \pm 3\pi/4\,. $

Da die Funktion auf ganz $ \mathbb{R}$ definiert und periodisch ist, sind keine Randwerte zu betrachten. Aus dem Vorzeichen der zweiten Ableitung

$\displaystyle f^{\prime\prime}(x) = 2 \sin x -12 \cos^2 x \, \sin x =2 \sin x(1-6\cos^2 x) $

und durch Vergleich der Funktionswerte läßt sich also der Typ der Extrema bestimmen:

\begin{displaymath} \begin{array}{c\vert c\vert c\vert l} x & f(x) & f''(x) & \... ...\sqrt{8}/3 & -2\sqrt{2}<0 & \mbox{globales Maximum} \end{array}\end{displaymath}

Wendepunkte: Die zweite Ableitung

$\displaystyle f^{\prime\prime}(x) = 2\sin x -12\cos^2 x \,\sin x=\sin x(6\sin^2x-5) $

ist Null für $ \sin x =0$ oder $ \sin x =\pm \sqrt{5/6}$, d.h.

$\displaystyle x=0 \quad\lor\quad x=\pm \pi \quad\lor\quad x=\pm a \quad\lor\quad x = \pm(\pi-a) $

mit $ a = \operatorname{arcsin}\sqrt{5/6}\approx {\tt 1.1503}$. Da die dritte Ableitung an diesen Stellen nicht verschwindet, hat $ f$ also Wendepunkte bei $ (0,0)$, $ (\pm \pi,0)$, $ (\pm a,\pm b)$ und $ (\pm(\pi-a),\pm b)$ mit

$\displaystyle b = f(a) = \sin a\,(2-(4/3)\sin^2 a) = \sqrt{5/6}\,(2-(4/3)(5/6)) \approx {\tt0.8114} \,, $

denn $ \sin a = \sin(\pi-a)$ und $ f(-a) = -f(a)$.

Asymptoten: Die Funktion ist periodisch und nicht konstant, hat also keine Asymptoten.

\includegraphics[width=10.4cm]{Kurvendiskussion_1}

siehe auch:

  automatisch erstellt am 15.  6. 2016