Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Real - und Imaginärteil

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Zeige: Eine komplexe Zahl $ \mbox{$z\in\mathbb{C}$}$ ist reell genau dann, wenn $ \mbox{$z = \bar z$}$. Eine komplexe Zahl $ \mbox{$z\in\mathbb{C}$}$ ist in $ \mbox{$\mathrm{i}\mathbb{R}$}$ (d.h. $ \mbox{$z = \mathrm{i}\, {\operatorname{Im}}(z)$}$) genau dann, wenn $ \mbox{$z = -\bar z$}$.

Zeige: Für alle $ \mbox{$z\in\mathbb{C}$}$ ist $ \mbox{$z^2 + z\bar z + \bar z^2\in\mathbb{R}$}$.

Zeige: Für alle $ \mbox{$z\in\mathbb{C}$}$ sind $ \mbox{$z + \bar z = 2{\operatorname{Re}}(z)$}$ und $ \mbox{$z - \bar z = 2\mathrm{i}\, {\operatorname{Im}}(z)$}$.

Lösung.

Ist $ \mbox{$z = x + \mathrm{i}y$}$ mit $ \mbox{$x,y\in\mathbb{R}$}$, so ist $ \mbox{$z = \bar z$}$ genau dann, wenn $ \mbox{$x + \mathrm{i}y = x - \mathrm{i}y$}$, d.h. wenn $ \mbox{$y = 0$}$ ist, d.h. $ \mbox{$z = x \in\mathbb{R}$}$.

Ferner ist $ \mbox{$z = -\bar z$}$ genau dann, wenn $ \mbox{$x + \mathrm{i}y = -x + \mathrm{i}y$}$, d.h. wenn $ \mbox{$x = 0$}$ ist, d.h. $ \mbox{$z =  \mathrm{i}y \in\mathrm{i}\mathbb{R}$}$.

Um den genannten Ausdruck als reell nachzuweisen, berechnen wir sein Konjugiertes. Es wird

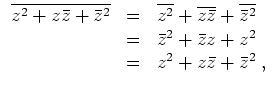
$ \mbox{$\displaystyle \begin{array}{rcl} \overline {z^2 + z\bar z + \bar z^2} ... ...z^2 + \bar z z + z^2 \\ & = & z^2 + z\bar z + \bar z^2\; , \\ \end{array}$}$
und somit $ \mbox{$z^2 + z\bar z + \bar z^2\in\mathbb{R}$}$.

Schließlich werden $ \mbox{$z + \bar z = (x + \mathrm{i}y) + (x - \mathrm{i}y) = 2x = 2{\operatorname{Re}}(z)$}$ und $ \mbox{$z - \bar z = (x + \mathrm{i}y) - (x - \mathrm{i}y) = 2\mathrm{i}y = 2\mathrm{i}\, {\operatorname{Im}}(z)$}$.

(Autoren: Künzer/Martin/Nebe)

siehe auch:

  automatisch erstellt am 25.  1. 2006