Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Abbildungen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Gegeben die Abbildung $ \mbox{$\mathbb{R}\unitlength.1mm\begin{picture}(80,50) \put( 0, 0){$\longrigh... ...w $} \put( 10, 27){\makebox[6mm]{$\scriptstyle f$}} \end{picture} \mathbb{R}$}$, $ \mbox{$x\mapsto f(x) = x^3 - x$}$.

(i)
Zeige, daß $ \mbox{$f$}$ nicht injektiv ist.
(ii)
Sei $ \mbox{$[1,\infty)\unitlength.1mm\begin{picture}(80,50) \put( 0, 0){$\longrigh... ...w $} \put( 10, 27){\makebox[6mm]{$\scriptstyle g$}} \end{picture} \mathbb{R}$}$, $ \mbox{$x\mapsto g(x) = x^3 - x$}$. (Man schreibt auch $ \mbox{$g = f\vert _{[1,\infty)}$}$ und sagt, $ \mbox{$g$}$ sei die Einschränkung von $ \mbox{$f$}$ auf $ \mbox{$[1,\infty)$}$.)

Zeige, daß $ \mbox{$g$}$ injektiv ist.

Lösung.

(i)
Es ist z.B. $ \mbox{$f^{-1}(\{ 0\}) = \{ -1,0,1\}$}$, da $ \mbox{$x^3 - x = (x-1)(x+1)x = 0$}$ diese drei Lösungen besitzt. Insbesondere ist $ \mbox{$\char93 f^{-1}(\{ 0\}) = 3 > 1$}$, und somit ist $ \mbox{$f$}$ nicht injektiv.

(ii)
Es genügt zu zeigen, daß aus $ \mbox{$x\geq 1$}$ und $ \mbox{$h > 0$}$ folgt, daß $ \mbox{$f(x) < f(x+h)$}$. Es wird
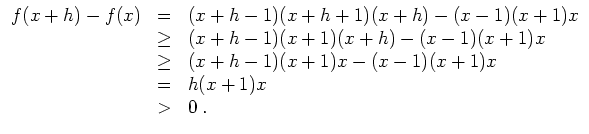
$ \mbox{$\displaystyle \begin{array}{rcl} f(x+h) - f(x) & = & (x+h-1)(x+h+1)(x+... ...h-1)(x+1)x - (x-1)(x+1)x \\ & = & h(x+1)x \\ & > & 0\; . \\ \end{array}$}$
(Autoren: Künzer/Martin/Nebe)

siehe auch:

  automatisch erstellt am 25.  1. 2006