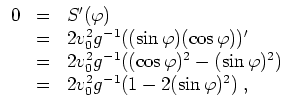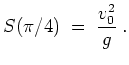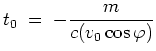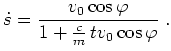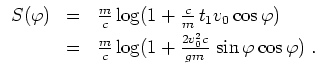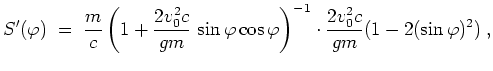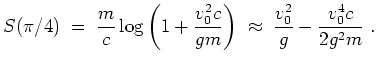Eine Kugel der Masse
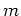 werde mit der Anfangsgeschwindigkeit
werde mit der Anfangsgeschwindigkeit
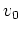 mit Abwurfwinkel
mit Abwurfwinkel
![$ \mbox{$\varphi \in [0,\pi/2]$}$](/inhalt/beispiel/beispiel952/img3.png) vom Boden aus geworfen.
Die Erdbeschleunigung sei
vom Boden aus geworfen.
Die Erdbeschleunigung sei
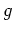 .
.
- (1)
- Berechne den Winkel
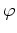 , für den die maximale Wurfweite erzielt wird. Gib die maximale Wurfweite an.
, für den die maximale Wurfweite erzielt wird. Gib die maximale Wurfweite an.
- (2)
- Selbes Problem wie (1), nur mit (vereinfachtem) Luftwiderstand. Es werde angenommen, daß dieser nur horizontal verursacht
wird und wirkt, d.h. daß auf die Kugel eine horizontale Kraft gegen die Wurfrichtung vom Betrag
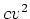 wirkt, wobei
wirkt, wobei
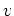 die
Horizontalgeschwindigkeit und
die
Horizontalgeschwindigkeit und
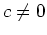 eine Konstante bezeichne.
eine Konstante bezeichne.
(Hinweis: Die Horizontalgeschwindigkeit ist von der Form
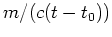 , wobei
, wobei
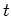 die Zeit bezeichnet, und
die Zeit bezeichnet, und
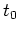 einen geeignet
zu wählenden Zeitpunkt.)
einen geeignet
zu wählenden Zeitpunkt.)
Lösung.
- (1)
- In Abhängigkeit von der Zeit beträgt die Vertikalgeschwindigkeit
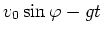 , woraus sich die Flughöhe
, woraus sich die Flughöhe
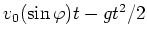 und der Aufprallzeitpunkt zu
und der Aufprallzeitpunkt zu
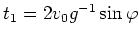 berechnet. In dieser Zeit wird die horizontale Strecke
zurückgelegt. Für die Randpunkte
berechnet. In dieser Zeit wird die horizontale Strecke
zurückgelegt. Für die Randpunkte
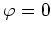 und
und
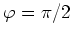 haben wir lokale Minima vorliegen.
Notwendig für Maximalität ist also
d.h.
haben wir lokale Minima vorliegen.
Notwendig für Maximalität ist also
d.h.
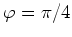 . Anhand von
. Anhand von
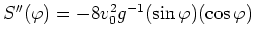 , und also von
, und also von
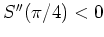 , erkennt man, daß
in der Tat ein Maximum vorliegt. Die maximale Wurfweite ist
, erkennt man, daß
in der Tat ein Maximum vorliegt. Die maximale Wurfweite ist
- (2)
- Der Aufprallzeitpunkt ist wie in (1) weiterhin
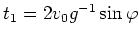 . Schreiben wir die Ableitung nach der Zeit mit
einem aufgestellten Punkt und die Wegstrecke als
. Schreiben wir die Ableitung nach der Zeit mit
einem aufgestellten Punkt und die Wegstrecke als
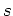 , so ergibt sich die Horizontalgeschwindigkeit
, so ergibt sich die Horizontalgeschwindigkeit
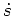 aus
aus
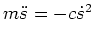 zu
wobei
zu
wobei
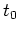 aus
aus
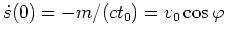 zu
resultiert. Also wird
Die zurückgelegte Wegstrecke zum Zeitpunkt
zu
resultiert. Also wird
Die zurückgelegte Wegstrecke zum Zeitpunkt
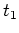 ergibt sich zu
Daraus erhalten wir
und also wiederum ein Maximum bei
ergibt sich zu
Daraus erhalten wir
und also wiederum ein Maximum bei
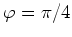 . Die maximale Wurfweite ist etwas kürzer, nämlich
Sei an dieser Stelle nochmal darauf hingewiesen, daß dieses Resultat unter der vereinfachenden Annahme, der Luftwiderstand
wirke nur horizontal und hänge auch nur von der Horizontalgeschwindigkeit ab, hergeleitet wurde.
. Die maximale Wurfweite ist etwas kürzer, nämlich
Sei an dieser Stelle nochmal darauf hingewiesen, daß dieses Resultat unter der vereinfachenden Annahme, der Luftwiderstand
wirke nur horizontal und hänge auch nur von der Horizontalgeschwindigkeit ab, hergeleitet wurde.
(Autoren: Künzer/Martin/Nebe)
| |
automatisch erstellt
am 25. 1. 2006 |


![]() werde mit der Anfangsgeschwindigkeit
werde mit der Anfangsgeschwindigkeit
![]() mit Abwurfwinkel
mit Abwurfwinkel
![]() vom Boden aus geworfen.
Die Erdbeschleunigung sei
vom Boden aus geworfen.
Die Erdbeschleunigung sei
![]() .
.
![]() , wobei
, wobei
![]() die Zeit bezeichnet, und
die Zeit bezeichnet, und
![]() einen geeignet
zu wählenden Zeitpunkt.)
einen geeignet
zu wählenden Zeitpunkt.)