Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Inverse Interpolation

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Aus Näherungen $ x_{\ell-n},\ldots,x_\ell$ für eine Nullstelle $ x_*$ einer Funktion $ f$ kann man eine Approximation $ x_{\ell+1}\approx x_*$ durch inverse Interpolation der Funktionswerte $ f_k = f(x_k)$ mit einem Polynom $ p$ vom Grad $ \leq n$ gewinnen. Sind $ f_k$ paarweise verschieden, so ist

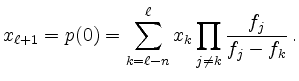
$\displaystyle x_{\ell+1} = p(0) = \sum_{k=\ell-n}^{\ell} x_k \prod_{j\ne k}\frac{f_j}{f_j-f_k} \,. $

\includegraphics[width=0.5\linewidth]{Bild_inverse_interpol.eps}

Die Iteration dieses Verfahrens ist für glatte Funktionen bei einfachen Nullstellen lokal konvergent und sehr effizient. Allerdings ist der Iterationsschritt nicht immer durchführbar. Die möglichen Ausnahmefälle müssen mit Hilfe eines anderen Verfahrens (z.B. Bisektion) überbrückt werden.

(Inhalt vorübergehend nicht verfügbar)
[Zurück]
  automatisch erstellt am 19.  8. 2013