Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Entwicklung einer Differentialgleichung im singulären Punkt

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Die Differentialgleichung

$\displaystyle r(z) u''(z) + q(z) u'(z) + p(z) u(z) = 0 $

hat bei $ z=a$ einen regulären singulären Punkt, wenn $ q/r$ einen Pol höchstens erster und $ p/r$ einen Pol höchstens zweiter Ordnung bei $ z=a$ haben.

In einem regulären singulären Punkt $ a$ wird das Verhalten der Lösungen $ u$ durch die charakteristische Gleichung

$\displaystyle \varphi(\lambda) = \lambda(\lambda-1) + q_0 \lambda + p_0 = 0 $

bestimmt, wobei $ q_0$ und $ p_0$ die führenden Koeffizienten von $ q/r$ bzw. $ p/r$ sind, d.h,

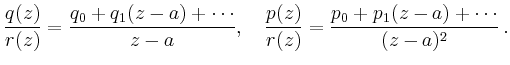
$\displaystyle \frac{q(z)}{r(z)} = \frac{q_0 + q_1 (z-a) + \cdots}{z-a},\quad \frac{p(z)}{r(z)} = \frac{p_0 + p_1 (z-a) + \cdots}{(z-a)^2}\,. $

Ist die Differenz der Nullstellen $ \alpha$, $ \beta$ von $ \varphi$ nicht ganzzahlig, so existieren zwei linear unabhängige Lösungen

$\displaystyle (z-a)^\alpha v(z),\quad (z-a)^\beta w(z) \,, $

wobei $ v$ und $ w$ in einer Umgebung von $ a$ analytische Funktionen mit $ v(a),w(a)\ne 0$ sind.

Sonst existiert im Allgemeinen nur eine Lösung dieses Typs zu dem Exponenten $ \alpha$ mit dem größten Realteil. Eine zweite Lösung kann dann durch Variation der Konstanten, d.h. mit dem Ansatz

$\displaystyle u(z) = c(z) (z-a)^\alpha v(z) $

bestimmt werden.

Zur formalen Rechtfertigung des Lösungstyps wird o. B. d. A. $ a=0$ sowie $ r(z)=1$ angenommen, und die Entwicklung

$\displaystyle u(z) = z^\lambda (u_0 + u_1 z + \cdots) $

in die Differentialgleichung substituiert. Der Vergleich des Koeffizienten von $ z^{\lambda-2}$ bei den Termen

$\displaystyle u''(z)$ $\displaystyle = \lambda(\lambda-1) u_0 z^{\lambda-2}+(\lambda+1)\lambda u_1 z^{\lambda-1} + \cdots,$    
$\displaystyle \frac{1}{z} u'(z) q(z)$ $\displaystyle = \left(\lambda u_0 z^{\lambda-2}+(\lambda+1) u_1 z^{\lambda-1} + \cdots \right) \left( q_0 +q_1 z + \cdots \right)\,,$    
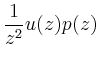$\displaystyle \frac{1}{z^2} u(z)p(z)$ $\displaystyle = \left( u_0 z^{\lambda-2}+ u_1 z^{\lambda-1} + \cdots \right) \left( p_0 +p_1 z + \cdots \right)\,,$    

führt auf

$\displaystyle \varphi(\lambda) u_0 = 0 \,, $

d.h. nicht triviale Lösungen $ \left(u_0\neq 0\right)$ können nur für Nullstellen von $ \varphi$ existieren. Der Vergleich der Koeffizienten von $ z^{\lambda-2+j}$ führt auf die Rekursion

$\displaystyle \varphi(\lambda+j) u_j = \psi(u_0,\ldots,u_{j-1})\,, \quad j>0 \,, $

mit

$\displaystyle \psi(u_0,\ldots,u_{j-1})$ $\displaystyle = -(\lambda q_ju_0+(\lambda+1)q_{j-1}u_1+\cdots+(\lambda+j-1)q_1u_{j-1})$    
  $\displaystyle \quad -(p_ju_0+p_{j-1}u_1+\cdots+p_1u_{j-1})\,.$    

Die Koeffizienten sind also sukzessive bestimmbar, falls $ \varphi(\lambda+j)\neq0$ für alle $ j$. Da $ \lambda$ eine Nullstelle von $ \varphi$ ist, ist dies nur dann nicht der Fall, wenn

$\displaystyle \lambda = \beta = \alpha-n $

mit $ n>0$ ist.
[Zurück]
  automatisch erstellt am 21. 11. 2013