Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Satz von Sylow; Sylowgruppen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Sei $ G$ eine endliche Gruppe, $ p$ eine Primzahl und $ \alpha \in \mathbb{N}_0$ mit $ \vert G\vert=p^\alpha \cdot n$, wobei $ \textrm{ggT}(p,n)=1$.
(a)
Existenz von Sylowgruppen
$ G$ besitzt mindestens eine Untergruppe der Ordnung $ p^\alpha$.

Die Untergruppen dieser Ordnung nennt man $ p-$Sylowgruppen von $ G$. Mit $ Syl_p(G)$ bezeichnet man die Menge der $ p-$Sylowgruppen von $ G$.

(b)
Eindeutigkeit von Sylowgruppen
Seien $ U,V \in Syl_p(G)$. Dann gibt es ein $ g \in G$ mit $ U^g=V$.

Verschiedene $ p-$Sylowgruppen sind also zueinander konjugiert. Somit sind die $ p-$Sylowgruppen bis auf einen inneren Automorphismus eindeutig bestimmt.

Ist $ W$ eine $ p-$Untergruppe von $ G$, d.h. eine Untergruppe mit $ \vert W\vert=p^b$, dann existiert eine $ p-$Sylowgruppe $ S$ von $ G$ mit $ W \leq S$.

(c)
Anzahl von Sylowgruppen
$ \vert Syl_p(G)\vert \equiv 1 \mod p$ und $ \vert Syl_p(G)\vert=\vert G:N_G(U)\vert$ für $ U \in Syl_p(G)\vert$.


Bemerkungen:

Für $ p \nmid \vert G\vert$ ist der Satz trivialerweise richtig. Ebenso für Gruppen von Primzahlpotenzordnung.
a)
Zunächst werden die folgenden Behauptungen bewiesen.

Behauptung 1: Ist $ G$ eine abelsche Gruppe mit $ \vert G\vert=n$ und $ p$ teilt $ n$, dann existiert ein Element $ x \in G$ mit $ o(x)=p$.

Beweis von Behauptung 1: Die Behauptung ist richtig, wenn $ G$ zyklisch ist, denn für $ G=\langle t \rangle$ und $ n=ps$ gilt $ (t^s)^p=1$ und $ t^s \neq 1$. Somit ist $ t^s$ ein Element der Ordnung $ p$.
Sei nun $ \vert G\vert=n$ und $ G$ ein minimales Gegenbeispiel. Wegen der Minimalität von $ G$ besitzt dann jede echte Untergruppe $ U$ von $ G$ $ p'-$Ordnung (d.h. $ p \nmid \vert U\vert$). Sei $ U <G$. Wegen $ p \mid \vert G\vert$ folgt $ p \mid \vert U\vert$ oder $ p \mid \vert G/U\vert$. Also gilt $ p \mid \vert G/U\vert$ und $ G/U$ hat ein Element $ xU$ der Ordnung $ p$, wobei $ xU$ das Bild von $ x \in G$ unter der Faktorabbildung $ \kappa: G \longrightarrow G/U$. Sei $ Z=\langle x \rangle$, dann ist $ \kappa(Z)=\langle xU \rangle \cong C_p$ eine zyklische Gruppe der Ordnung $ p$ und wegen $ Z/\left(Ker(\kappa) \cap Z \right) \cong C_p$ folgt, dass $ p$ die Ordnung von $ Z$ teilt. Wiederum wegen der Minimalität von $ G$ folgt dann, dass $ Z$ ein Element der Ordnung $ p$ besitzt, und damit auch $ G$. Also gibt es kein minimales Gebenbeispiel.

Behauptung 2: Sei $ G$ ein kleinstes Gegenbeispiel zu Teil a) des Sylowsatzes, dann gilt $ p \mid \vert Z(G)\vert$.

Beweis von Behauptung 2: Man kann $ G$ als nicht-abelsch annehmen. Des Weiteren gilt $ p \mid \vert G\vert$, da der Satz für $ p \nmid \vert G\vert$ wahr ist. Für die Operation von $ G$ auf sich selbst durch Konjugation gilt die Klassengleichung

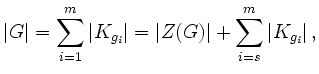
$\displaystyle \vert G\vert= \sum \limits_{i=1}^m \vert K_{g_i}\vert= \vert Z(G)\vert+\sum \limits_{i=s}^m \vert K_{g_i}\vert \,, $

wobei $ K_{g_i}$ die Konjugiertenklasse von $ G$ mit dem Repräsentanten $ g_i$ ist, $ \{g_1, \ldots, g_{s-1}\}$ ein Repräsentantensystem der Klassen von Länge $ 1$ und $ \{g_s, \ldots, g_{m}\}$ ein Repräsentantensystem der Klassen von Länge größer als $ 1$.

Angenommen es existiert ein Index $ j$ mit $ (p,\vert K_{g_i}\vert)=1$ (für $ s \leq j \leq m$). Nach dem Bahnenlemma gilt

$\displaystyle \vert K_{g_j}\vert=\vert G/C_G(g_j)\vert\,. $

Wegen $ (p,\vert K_{g_i}\vert)=1$ folgt dann, dass $ p^\alpha \nmid \vert G(C_G(g_j)\vert$, also gilt $ p^\alpha \mid \vert C_G(g_j)\vert$. Da $ G$ ein kleinstes Gegenbeispiel und $ \vert C_G(g_j)\vert < \vert G\vert$ ist folgt, dass $ C_G(g_j)$ $ p-$Sylowgruppen der Ordnung $ p^\alpha$ hat. Damit besitzt aber auch $ G$ solche Untergruppen und ist daher kein Gegenbeispiel. Also folgt $ p \mid \vert K_{g_j}\vert$ für alle $ j\geq s$, und damit $ p \mid \vert Z(G)\vert$.

Behauptung 3: Sei $ \varphi: G \longrightarrow H$ ein surjektiver Homomorphismus. Ist $ U \leq H$, dann ist $ \varphi(U) \leq G$. Ist $ G$ endlich, dann gilt $ \vert\varphi^{-1}(U)\vert=\vert U\vert \cdot \vert Ker (\varphi)\vert$.

Beweis von Behauptung 3: Sind $ x,y \in \varphi^{-1}(U)$, dann ist $ \varphi(xy^{-1})=\varphi(x)\varphi(y)^{-1}$. Damit ist $ xy^{-1}\in \varphi^{-1}(U)$ und nach dem Untergruppenkriterium ist $ \varphi^{-1}(U)\leq G$.

Man beachte, dass $ \varphi^{-1} (U)\supseteq Ker \varphi$ ist, denn $ \varphi(Ker(\varphi))=1 \leq U$ und $ \varphi(\varphi^{-1}(U))=U$, da $ \varphi$ surjektiv. Nach dem Homomorphisatz ist $ \varphi^{-1}(U)/Ker(\varphi) \cong U$ und damit

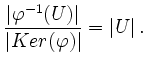
$\displaystyle \frac{\vert\varphi^{-1}(U)\vert}{\vert Ker(\varphi)\vert}=\vert U\vert \,. $

Beweisabschluss von Teil a): Sei $ G$ ein kleinster Verbrecher. Nach Behauptung 2 gilt $ Z(G) \neq 1$ und $ p \mid \vert Z(G)\vert$. Nach Behauptung 1 existiert ein Element $ x\in Z(G)$ mit $ o(x)=p$. Damit folgt, dass $ Z(G) \cong C_p$ zyklisch ist und $ \langle x \rangle \vartriangleleft G$, da $ x$ zentral. Man beachte, dass $ \langle x \rangle \neq G$ gilt, da $ G$ keine $ p-$Gruppe ist. Betrachte nun die Abbildung

$\displaystyle \varphi \ : \ g \longrightarrow G/ \langle x \rangle \,. $

Nach Voraussetzung ist $ G/\langle x \rangle $ kein Verbrecher, und es gilt

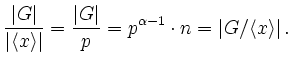
$\displaystyle \displaystyle{ \frac{\vert G\vert}{\vert\langle x \rangle\vert} =... ...c{\vert G\vert}{p}=p^{\alpha-1} \cdot n = \vert G/ \langle x \rangle\vert} \,. $

Es existiert also eine Sylowgruppe $ U$ von $ G/\langle x \rangle $ mit $ \vert U\vert=p^{\alpha-1}$. Nach Behauptung 3 ist

$\displaystyle \varphi^{-1}(U)=p \cdot p^{\alpha-1}=p^{\alpha} \,. $

Damit hat $ G$ eine $ p-$Sylowgruppe und es existiert kein kleinster Verbrecher. Teil a) ist damit bewiesen.

b)
Sei $ W$ eine $ p-$Untergruppe von $ G$ und $ P \in Syl_p(G)=M$. Setze $ \widetilde{M}= \{ P^g \ ; \ g\in G \}$. Nach dem Bahnenlemma gilt $ \vert\widetilde{M}\vert=\vert G/N_G(P)\vert$. Wegen $ \vert P\vert=p^\alpha$ it $ p$ kein Teiler von $ \vert\widetilde{M}\vert$. Andererseits operiert $ W$ via Konjugation auf $ \widetilde{M}$. Da $ W$ eine $ p-$Gruppe ist besitzen alle Bahnen der $ W-$Operation Längen der Form $ p^\gamma$ mit $ \gamma \in {\mathbb{N}}_0$.

Angenommen es ist $ \gamma \geq 1$, dann ist $ \vert\widetilde{M}\vert \equiv 0 \mod p$, im Widerspruch zu $ p \nmid \vert\widetilde{M}\vert$. Also existiert ein $ \widetilde{P}=P^{g_0}$ mit $ \widetilde{P}^x= \widetilde{P}$ für alle $ x \in W$ und es ist $ W \leq N_G(\widetilde{P})$. Weiter ist $ \widetilde{P} \unlhd N_G(\widetilde{P})$. Betrachte nun $ \widetilde{P} \cdot W$. Dann ist $ \widetilde{P} \cdot W$ eine Untergruppe von $ N_G(\widetilde{P})$, da $ \widetilde{P} \unlhd N_G(\widetilde{P})$. Nach dem Isomorphisatz folgt $ \widetilde{P} \cdot W=\widetilde{P}$ und damit $ W \leq \widetilde{P}$.

Führt man den Beweis mit $ U=P$ und $ V=W$, dann ergibt sich die Konjugiertheit von verschiedenen $ p-$Sylowgruppen (insbesondere ist $ M=\widetilde{M}$).

c)
Ist $ S \in Syl_p(G)$, dann kann es nur eine Bahn der Länge $ 1$ bei der $ S-$Operation auf $ M$ geben, denn aus $ P=\widetilde{S}_1$ und $ P=\widetilde{S}_2$ folgt $ S_1=S_2$. Also ist

$\displaystyle \vert Syl_p(G)\vert \equiv 1 \mod p \,.$

Der zweite Teil von c) folgt mit dem Bahnenlemma, denn es gilt $ Syl_p(G)=M$ und $ \vert M\vert=\vert G/N_G(S)\vert$.

(Autoren: Höfert/Kimmerle )
[Zurück zur Aussage]
  automatisch erstellt am 17. 10. 2006