Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Cauchy-Frobenius-Lemma, "Lemma von Burnside"

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Sei $ X$ eine endliche $ G-$Menge und $ m$ die Anzahl der Bahnen von $ X$.
Für $ g\in G$ bezeichne $ \chi(g)$ die Anzahl der Elemente von $ X$, die von $ g$ fixiert werden, d.h. $ \chi(g)=\vert\{x\in X \ ; \ gx=x \}\vert$. Dann gilt

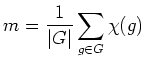
$\displaystyle m=\frac{1}{\vert G\vert}\sum \limits_{g\in G}\chi(g) $

Bemerkung: Das Lemma wird fälschlicherweise oft ''Lemma von Burnside'' genannt. Da diese Bezeichnung sehr weit verbreitet ist, heißt es manchmal auch scherzhaft "das Lemma das nicht von Burnside ist".

Im folgenden Beweis bezeichnet $ G_x=\{ g\in G \ ; gx=x\}$ den Punktstabilisator eines Elements $ x\in X$, $ \{B_1 , \ldots , B_m\}$ die Bahnen unter der Operation von $ G$ und $ x_i$ einen Repräsentanten der Bahn $ B_i$.

Wird $ x$ von $ g$ fixiert, dann ist umgekehrt $ g\in G_x$. Man erhält die Gleichung

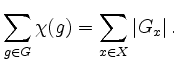
$\displaystyle \sum\limits_{g \in G} \chi (g)=\sum \limits_{x \in X} \vert G_x\vert \,. $

Diese Summe kann nun in die einzelnen Bahnen aufgespalten werden. Beachtet man dabei, dass die Punktstabilisatoren innnerhalb einer Bahn gleich groß sind, so ergibt sich

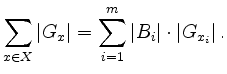
$\displaystyle \sum \limits_{x \in X} \vert G_x\vert=\sum \limits_{i=1}^m \vert B_i\vert\cdot \vert G_{x_i}\vert \,. $

Verwendet man nun, dass die Länge der Bahn gleich dem Index des Punktstabilisators in $ G$ ist, dann sieht man, dass

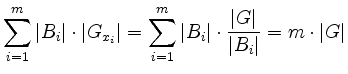
$\displaystyle \sum \limits_{i=1}^m \vert B_i\vert\cdot \vert G_{x_i}\vert= \sum... ... \vert B_i\vert \cdot \frac{\vert G\vert}{\vert B_i\vert}=m\cdot \vert G\vert $

gilt. Insgesamt ist also

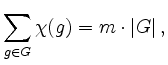
$\displaystyle \sum\limits_{g \in G} \chi (g)=m\cdot \vert G\vert \,, $

und die Behauptung ist gezeigt.
[Zurück zur Aussage]
  automatisch erstellt am 17.  1. 2008