Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Eigenschaften von Kommutatoren

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Sei $ G$ eine Gruppe. Die Kommutatoren von $ G$ besitzen die folgenden Eigenschaften.

a)
$ [G,G]$ ist ein Normalteiler von $ G$.

Die Gruppe $ G \, / \, [G,G]$ heißt Kommutatorfaktorgruppe. Sie ist das größte abelsche Bild von $ G$, d.h. ist $ \varphi: \ G \rightarrow H$ ein Gruppenhomorphismus und $ \varphi(G)$ ist abelsch, dann gibt es eine zu $ \varphi(G)$ isomorphe Untergruppe der Kommutatorfaktorgruppe. Wegen dieser Eigenschaft nennt man die Kommutatorfaktorgruppe auch die ,abelsch gemachte Gruppe.

b)
Für $ M,N \unlhd G$ gilt $ [M,N] \unlhd G$.
c)
Sei $ \varphi: \ G \longrightarrow H$ ein Gruppenhomomorphismus und $ M,N \subseteq G$. Dann ist

$\displaystyle \varphi([M,N])=[\varphi(M),\varphi(N)]. $

b)
Zunächst wird Teil b) bewiesen. Die Menge ist $ [M,N]$ per Definition eine Untergruppe von $ G$. Sei nun $ g \in G, m\in M$ und $ n\in N$. Dann ist

$\displaystyle g^{-1}m^{-1}n^{-1}mng=\underbrace{g^{-1}m^{-1}g}_{=\tilde{m}^{-1}... ...e{m}} \underbrace{g^{-1}ng}_{=\tilde{n}} = [\tilde{m},\tilde{n}] \in [M,N] \,. $

Da die Kommutatoren der Form $ [m,n]$ die Gruppe $ [M,N]$ erzeugen ist $ g^{-1}[M,N]g=[M,N]$ und damit ist $ [M,N]$ normal in $ G$.
a)
Der erste Teil der Aussage ist ein Spezialfall von b) mit $ M=N=G$.

Setzt man $ G'=[G,G]$, dann gilt

$\displaystyle gG' \cdot hG'=ghG'=ghh^{-1}g^{-1}hgG'=hgG'=hG' \cdot gG' \,. $

Damit ist $ G/G'$ abelsch.

Sei nun $ A$ irgendein abelsches Bild von $ G$, d.h. es existiert ein surjektiver Gruppenhomomorphismus $ \varphi \ : \ G \longrightarrow A$. Dann gilt

$\displaystyle \varphi(g_1^{-1}g_2^{-1}g_1g_2)=\varphi(g_1)^{-1}\varphi(g_2)^{-1}\varphi(g_1) \varphi(g_2)=1 \,, $

da $ A$ abelsch ist. Damit folgt $ G' \subseteq Ker(\varphi)$.

Man definiert nun die Abbildung

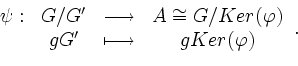
\begin{displaymath} \begin{array}{cccc} \psi : & G/G' & \longrightarrow & A \con... ...arphi) \\ & gG'& \longmapsto & g Ker(\varphi) \end{array}\,. \end{displaymath}

$ \psi$ ist wohldefiniert, da $ G' \subseteq Ker(\varphi)$ ist und $ \psi$ ist offensichtlich ein surjektiver Gruppenhomomorphismus.

Insgesamt folgt also, dass $ G/G'$ das größte abelsche Bild von $ G$ ist.

c)
Es sei $ m \in M$ und $ n\in N$. Dann ist

\begin{displaymath} \begin{array}{lcl} \varphi([m,n])&=&\varphi(m^{-1}n^{-1}mn)\... ...phi(m)\varphi(n)\\ &=& [\varphi(m),\varphi(n)] \,. \end{array}\end{displaymath}

[Zurück zur Aussage]
  automatisch erstellt am 31. 10. 2006