
Mathematik-Online-Lexikon: Erläuterung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: Erläuterung zu | |
Zusammenhang zwischen zweikantengefärbeten Graphen und den Teilmengen von endlichen Mengen |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
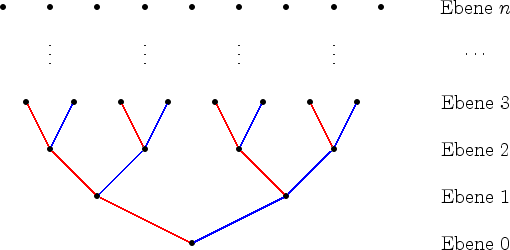
Das Bild von ![]() in
in ![]() wird folgendermaßen konstruiert:
wird folgendermaßen konstruiert:
Man durchläuft den Graphen ![]() von unten nach oben bis zur Ebene
von unten nach oben bis zur Ebene ![]() . Beim Schritt von der Ebene
. Beim Schritt von der Ebene ![]() zur
Ebene
zur
Ebene ![]() wählt man eine blaue Kante, falls
wählt man eine blaue Kante, falls ![]() gilt, anderenfalls eine rote. Auf diese Weise erhält man
z.B. für
gilt, anderenfalls eine rote. Auf diese Weise erhält man
z.B. für ![]() und
und
![]() in
in ![]() den Weg:
den Weg:
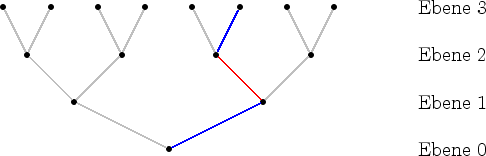
Mit Hilfe dieser Abbildung lässt sich zeigen:
Die Anzahl der ![]() -elementigen Teilmenge einer Menge mit
-elementigen Teilmenge einer Menge mit ![]() Elementen ist
Elementen ist
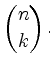
Bei einer ![]() -elementigen Menge kann man ohne Einschränkung von der Menge
-elementigen Menge kann man ohne Einschränkung von der Menge
![]() ausgehen. Die oben
definierte Abbildung von
ausgehen. Die oben
definierte Abbildung von ![]() nach
nach ![]() zeigt, dass die Anzahl der
zeigt, dass die Anzahl der ![]() -elementigen Teilmengen
-elementigen Teilmengen
![]() die gleiche ist, wie die Anzahl der Wege in
die gleiche ist, wie die Anzahl der Wege in ![]() bis zur Ebene
bis zur Ebene ![]() mit
mit ![]() blauen Kanten. Man beweist also:
blauen Kanten. Man beweist also:
Die Anzahl der Wege in ![]() bis Ebene
bis Ebene ![]() die genau
die genau ![]() blaue Kanten besitzen ist
blaue Kanten besitzen ist
![]() . Den Beweis
führt man mit Induktion nach
. Den Beweis
führt man mit Induktion nach ![]() für ein festes
für ein festes ![]() .
.
Induktionsanfang: Die Aussage macht nur für ![]() Sinn. Sei also
Sinn. Sei also ![]() . Es gilt
. Es gilt
![]() und
es gibt genau einen Weg bis zur Ebene
und
es gibt genau einen Weg bis zur Ebene ![]() , der
, der ![]() blaue Kanten besitzt.
blaue Kanten besitzt.
Induktionsvoraussetzung: Bis zur Ebene ![]() gibt es
gibt es
![]() Wege die genau
Wege die genau ![]() blaue Kanten besitzen.
blaue Kanten besitzen.
Induktionsschritt: Wir suchen die Wege bis zur Ebene ![]() von
von ![]() , die genau
, die genau ![]() blaue Kanten
enthalten. Dazu betrachtet man in
blaue Kanten
enthalten. Dazu betrachtet man in ![]() die beiden Bereiche
die beiden Bereiche ![]() und
und ![]()
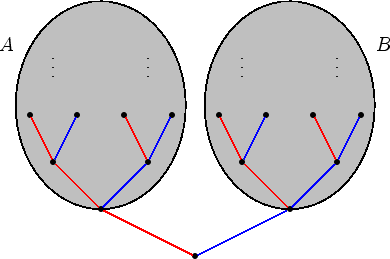
Die Teile des Graphen ![]() die in
die in ![]() , bzw.
, bzw. ![]() liegen, entsprechen jeweils dem Graphen
liegen, entsprechen jeweils dem Graphen ![]() . Ein Weg in
. Ein Weg in
![]() verläuft nun stets entweder durch
verläuft nun stets entweder durch ![]() oder durch
oder durch ![]() .
.
Bei jedem Weg mit ![]() blauen Kanten von
blauen Kanten von ![]() der teilweise durch
der teilweise durch ![]() verläuft müssen alle
verläuft müssen alle ![]() blauen
Kanten bereits in
blauen
Kanten bereits in ![]() liegen, denn zwischen den Ebenen 0 und
liegen, denn zwischen den Ebenen 0 und ![]() von
von ![]() wird der Weg durch eine rote
Kante vervollständigt. Nach Induktionsvoraussetzung gibt es in
wird der Weg durch eine rote
Kante vervollständigt. Nach Induktionsvoraussetzung gibt es in ![]() genau
genau
![]() Wege mit
Wege mit ![]() blauen
Kanten.
blauen
Kanten.
Bei jedem Weg der teilweise durch ![]() verläuft müssen
verläuft müssen ![]() blaue Kanten in
blaue Kanten in ![]() liegen, denn zwischen den
Ebenen 0 und
liegen, denn zwischen den
Ebenen 0 und ![]() von
von ![]() wird der Weg durch eine blaue Kante vervollständigt. Nach
Induktionsvoraussetzung gibt es in
wird der Weg durch eine blaue Kante vervollständigt. Nach
Induktionsvoraussetzung gibt es in ![]() genau
genau
![]() Wege mit
Wege mit ![]() blauen Kanten.
blauen Kanten.
Die Anzahl der Wege in ![]() mit
mit ![]() blauen Kanten ist also
blauen Kanten ist also
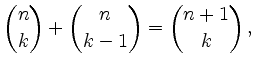
| automatisch erstellt am 26. 2. 2007 |