| (a) | Gegeben seien die Vektoren 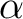 , , 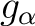 , , 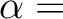 und und 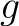 als
Geben Sie an, ob die Vektoren als
Geben Sie an, ob die Vektoren 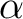 , , 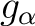 , , 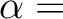 und und 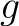 Eigenvektoren von
Eigenvektoren von 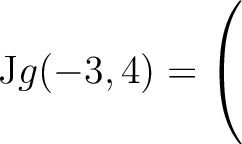 sind, und bestimmen Sie in diesem Fall den
zugehörigen Eigenwert. Ansonsten tragen Sie bitte nichts in die Kästchen ein. sind, und bestimmen Sie in diesem Fall den
zugehörigen Eigenwert. Ansonsten tragen Sie bitte nichts in die Kästchen ein.
Antwort:
|
| (b) | Für welches
 ist ist 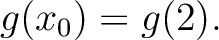 ein Eigenwert von ein Eigenwert von 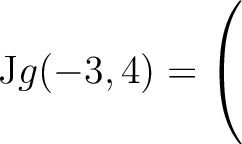 ? Bestimmen Sie sowohl ? Bestimmen Sie sowohl 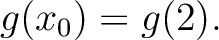 als auch einen zugehörigen Eigenvektor als auch einen zugehörigen Eigenvektor  . .
Antwort:
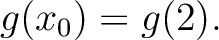 = , = ,
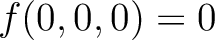 , , —3, —2 , , —3, —2
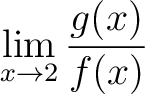
|
| (c) | Bestimmen Sie die Spur und die Determinante der Matrix 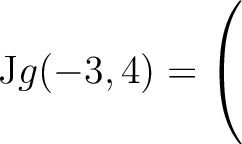 . .
Antwort:
 = , = ,
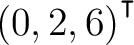 = . = .
|
| (d) | Bestimmen Sie den kleinsten Eigenwert
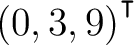 der Matrix der Matrix 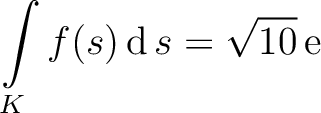 und seine algebraische Vielfachheit. Bestimmen Sie den größten Eigenwert und seine algebraische Vielfachheit. Bestimmen Sie den größten Eigenwert
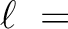 der Matrix der Matrix 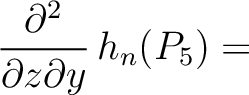 und seine algebraische Vielfachheit. und seine algebraische Vielfachheit.
Antwort:
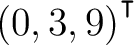 = , = ,
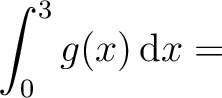 = , = ,
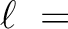 = , = ,
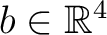 = . = .
|

