
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1589: Shuttle-Flug |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Schreiben Sie ein MATLAB-Programm shuttle, das die durch
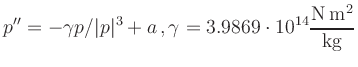
function shuttle(r,time_factor)
% shuttle flight
% r [= 20000]: distance of stationary orbit
% time_factor [= 1/500]: ratio to real time
% control flight using arrow keys:
% left/right, up = accelerate, down = brake
% force ~ number of consecutive key strokes
global A Amin GAMMA;
if nargin < 2;
time_factor = 1/500;
if nargin < 1;
r = 20000;
end;
end;
% parameters
GAMMA = 398690;
r_earth = 6378;
pts_orbit = 100;
Amin = GAMMA/(r_earth.^2*10);
mode = {'slower', 'right', 'off', 'left', ...
'faster'};
u = [r; 0; 0; sqrt(GAMMA/r)];
A = [0; 0];
dt = 2*pi*sqrt(r_earth.^3/GAMMA)/pts_orbit;
figure;
% identify key-function
set(gcf,'KeyPressFcn','key_action');
axis equal; hold on;
% draw earth
theta = 2*pi*linspace(0,1);
fill(r_earth*cos(theta),r_earth*sin(theta),'b');
while length(A)>0;
% time step
[t, udt] = ode45(@fct,[0 dt],u);
plot([u(1) udt(end,1)],[u(2) udt(end,2)],'r');
u = udt(end,:)';
% show current parameter values
f = num2str(round(norm(A)/Amin));
v = num2str(round(1000*norm(u(3:4))));
xlabel(['velocity: ' v ' ' ...
mode{3+[2,1]*sign(A)} ' ' f]);
% check distance to planet
if norm(u(1:2)) < r_earth;
return;
end;
pause(dt*time_factor);
end;
hold off;
%%%%%
function key_action()
% changes thrust value and direction
% according to keys pressed
global A Amin;
key = double(get(gcf,'CurrentCharacter'));
switch key
case 28 % left
if A(2) >= 0 & A(1) == 0
A = A+[0; Amin];
else
A = 0*A;
end;
case 29 % right
if A(2) <= 0 & A(1) == 0
A = A-[0; Amin];
else
A = 0*A;
end;
case 30 % up
if A(1) >= 0 & A(2) == 0
A = A+[Amin; 0];
else
A = 0*A;
end;
case 31 % down
if A(1) <= 0 & A(2) == 0
A = A-[Amin; 0];
else
A = 0*A;
end;
otherwise
A = [];
end;
%%%%%
function du = fct(t,u)
% equations of motion for shuttle flight
global A GAMMA;
p = u(1:2);
v = u(3:4);
w = [-v(2); v(1)];
du = [v; -GAMMA*p/norm(p).^3];
du(3:4) = du(3:4) + [v, w]*A/(1/10+norm(v));
| automatisch erstellt am 13. 2. 2008 |