
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Interaktive Aufgabe 287: HM I/II Vorbereitungskurs |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Mit
![]() und
und
![]() ist
ist
![]() ein Normmalenvektor zu
ein Normmalenvektor zu ![]() . Es
gilt dazu:
. Es
gilt dazu:
![]() . Die Hessesche Normalform ist also:
. Die Hessesche Normalform ist also:
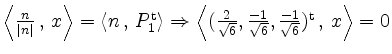
![]() besitzt die Parameterdarstellung:
besitzt die Parameterdarstellung:
![]() wobei
wobei
![]() ist.
ist.
Das Einsetzen in
![]() ergibt:
ergibt:
![]() und
und
![]() .
.
![]() ist ein
Richtungsvektor von
ist ein
Richtungsvektor von ![]() und steht zum Normallenvektor
und steht zum Normallenvektor
![]() von
von ![]() senkrecht. Es gilt also
senkrecht. Es gilt also
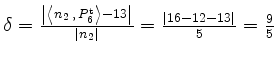
| automatisch erstellt am 10. 7. 2008 |