Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Differentiation komplexer Funktionen zu

Aufgabe 254: Orte komplexer Differenzierbarkeit

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

In welchen Punkten $ \mbox{$z = x+\mathrm{i}y$}$, $ \mbox{$x,y$}$ reell, ist $ \mbox{$f(z) = u(x,y) + \mathrm{i}v(x,y)$}$ komplex differenzierbar, wenn man

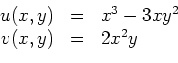\begin{displaymath}\begin{array}{rcl} u(x,y) & = & x^3 - 3 x y^2 \\ v(x,y) & = & 2x^2 y \\ \end{array}\end{displaymath}    

setzt?

Gib ein reelles Polynom $ \mbox{$\tilde{v}(x,y)$}$ in $ \mbox{$x$}$ und $ \mbox{$y$}$ an, so daß $ \mbox{$\tilde{f}(z) = u(x,y) + \mathrm{i}\tilde{v}(x,y)$}$ auf ganz $ \mbox{$\mathbb{C}$}$ komplex differenzierbar ist.

Es gilt

$ \mbox{$\displaystyle \begin{array}{rcl} u_x &=& 3x^2 - 3y^2,\\ u_y &=& -6 xy,\\ v_x &=& 4xy,\\ v_y &=& 2x^2.\\ \end{array}$}$
Die zweite der Cauchy-Riemannschen Differentialgleichungen verlangt $ \mbox{$xy = 0$}$. Die erste verlangt $ \mbox{$x^2 = 3y^2$}$. Damit ist $ \mbox{$f$}$ in $ \mbox{$z = 0$}$ differenzierbar und nirgendwo sonst.

Für ein solches Polynom $ \mbox{$\tilde{v}(x,y)$}$ muß wegen der ersten Cauchy-Riemannschen Differentialgleichung $ \mbox{$\tilde{v}_y(x,y) = 3x^2 - 3y^2$}$ gelten, d.h. $ \mbox{$\tilde{v}(x,y) = 3x^2 y - y^3 + c(x)$}$, $ \mbox{$c(x)$}$ ein reelles Polynom in $ \mbox{$x$}$. Die zweite verlangt dann $ \mbox{$c'(x) = 0$}$. Somit können wir $ \mbox{$\tilde{v}(x,y) = 3x^2 y - y^3$}$ wählen.

Es wird so im übrigen $ \mbox{$\tilde{f}(z) = z^3$}$.

(Autoren: Künzer/Meister/Nebe)
[Zurück zur Aufgabe]
  automatisch erstellt am 7.  6. 2005