Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Kombinatorik (Ziehung aus Urne) zu

Aufgabe 268: Kombinatorik (Ziehung aus Urne)

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Eine Urne werde nacheinander mit $ \mbox{$N$}$ Kugeln bestückt, deren Farbe jeweils mit Wahrscheinlichkeit $ \mbox{$\frac{1}{2}$}$ entweder weiß oder schwarz sei.

(i)
Sei $ \mbox{$0\leq k \leq N$}$. Bestimme die Wahrscheinlichkeit, daß die Urne mit $ \mbox{$k$}$ weißen Kugeln bestückt wird.

(ii)
Die Urne sei mit $ \mbox{$k$}$ weißen Kugeln bestückt. Sei $ \mbox{$0\leq n < k$}$. Man habe $ \mbox{$n$}$ Kugeln zufällig entnommen und dabei nur weiße Kugeln erhalten. Bestimme die Wahrscheinlichkeit, mit der auch die $ \mbox{$(n+1)$}$-te zufällig entnommene Kugeln weiß ist.

(iii)
Sei $ \mbox{$0\leq n < N$}$. Man habe $ \mbox{$n$}$ Kugeln zufällig entnommen und dabei nur weiße Kugeln erhalten. Bestimme die Wahrscheinlichkeit, daß auch die $ \mbox{$(n+1)$}$-te zufällig entnommene Kugeln weiß ist.

(i)
Es werden aus $ \mbox{$N$}$ Kugeln $ \mbox{$k$}$ Kugeln ausgewählt, die eine weiße Farbe erhalten. Die Anzahl der Möglichkeiten hierfür beträgt somit $ \mbox{$\binom{N}{k}$}$. Die Wahrscheinlichkeit für das Ereignis $ \mbox{$W_k$}$, daß die Urne mit $ \mbox{$k$}$ weißen Kugeln bestückt ist, beträgt folglich
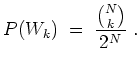
$ \mbox{$\displaystyle P(W_k) \; =\; \frac{\binom{N}{k}}{2^N}\; . $}$

(ii)
Sei $ \mbox{$A_j$}$ das Ereignis, daß die ersten $ \mbox{$j$}$ gezogenen Kugeln weiß sind. Beachte $ \mbox{$A_1\supseteq A_2\supseteq\dots$}$.

Gesucht ist nun die Wahrscheinlichkeit $ \mbox{$p(A_{n+1}\vert A_n\cap W_k)$}$, mit der also $ \mbox{$A_{n+1}$}$ unter den Voraussetzungen $ \mbox{$W_k$}$ (Urne mit $ \mbox{$k$}$ weißen Kugeln) und $ \mbox{$A_n$}$ (bereits $ \mbox{$n$}$ weiße gezogen) eintritt.

Dazu berechnen wir zunächst $ \mbox{$P(A_j\vert W_k)$}$ zu

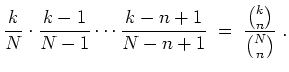
$ \mbox{$\displaystyle \frac{k}{N}\cdot\frac{k-1}{N-1}\cdots \frac{k-n+1}{N-n+1} \; =\; \frac{\binom{k}{n}}{\binom{N}{n}} \; . $}$
Es gilt also für $ \mbox{$n\leq k$}$
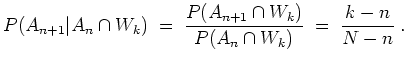
$ \mbox{$\displaystyle P(A_{n+1}\vert A_n\cap W_k)\; =\; \frac{P(A_{n+1}\cap W_k)}{P(A_n\cap W_k)}\; =\; \frac{k-n}{N-n}\; . $}$

(iii)
Es ist $ \mbox{$P(A_{n+1}\vert A_n) = \frac{P(A_{n+1})}{P(A_n)}$}$ zu bestimmen. Es gilt mit (ii)
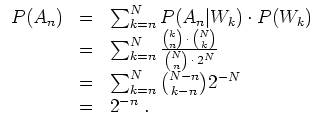
$ \mbox{$\displaystyle \begin{array}{rcl} P(A_n) & = & \sum_{k = n}^N P(A_n\v... ... \sum_{k = n}^N \binom{N-n}{k-n} 2^{-N} \\ & = & 2^{-n}\; . \end{array} $}$
Damit ist $ \mbox{$P(A_{n+1}\vert A_n) = \frac{1}{2}$}$.

Dies ist auch von vorneherein klar, da man die Kugeln bei der Bestückung der Urne und beim Ziehen als ungefärbt, und die Farbgebung als danach stattfindend annehmen darf. Dann ist die Farbe der $ \mbox{$(n + 1)$}$ten Kugel natürlich unabhängig von der Farbe der vorhergehenden. Beachte aber, daß diese Überlegung für (ii) nicht anwendbar ist - es hängt $ \mbox{$P(A_{n+1}\vert A_n\cap W_k)$}$ von $ \mbox{$k$}$ und von $ \mbox{$n$}$ ab.

(Autoren: Künzer/Meister/Nebe)
[Zurück zur Aufgabe]
  automatisch erstellt am 7.  6. 2005