
Mathematik-Online-Aufgabensammlung: Ungleichung von Chebyshev (Münzwurf) zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Ungleichung von Chebyshev (Münzwurf) zu | |
Aufgabe 271: Ungleichung von Chebyshev (Münzwurf) |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Wie oft muß eine Münze mindestens geworfen werden, damit mit einer
Wahrscheinlichkeit von mindestens
![]() die relative Häufigkeit von Kopf vom
erwarteten Wert
die relative Häufigkeit von Kopf vom
erwarteten Wert
![]() um weniger als
um weniger als
![]() abweicht?
Approximiere mit Hilfe der Chebyshevschen Ungleichung.
abweicht?
Approximiere mit Hilfe der Chebyshevschen Ungleichung.
Der Münzwurf wird durch eine Folge unabhängiger Zufallsvariablen
![]() beschrieben mit
beschrieben mit
![]() .
.
Gesucht ist
![]() minimal, so daß
minimal, so daß
![]() ,
oder äquivalent,
,
oder äquivalent,
Es gilt
![]() und
und
![]() .
Die Chebyshevsche Ungleichung ergibt
.
Die Chebyshevsche Ungleichung ergibt
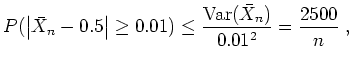
| automatisch erstellt am 7. 6. 2005 |