
Mathematik-Online-Aufgabensammlung: Approximation (Poisson, Moivre-Laplace) zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Approximation (Poisson, Moivre-Laplace) zu | |
Aufgabe 272: Approximation (Poisson, Moivre-Laplace) |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Ein Verteter wird erfahrungsgemäß bei einem Erstbesuch mit einer
Wahrscheinlichkeit
![]() eine Verkauf abschließen.
eine Verkauf abschließen.
Wie groß ist die (approximative) Wahrscheinlichkeit dafür,
daß er bei
![]() Erstbesuchen mindestens
Erstbesuchen mindestens
![]() , aber höchstens
, aber höchstens
![]() Verkäufe abschließt? Berechne sowohl mit de Moivre-Laplace und
(ggf. mit Rechnerunterstützung auch mit der Poissonapproximation).
Verkäufe abschließt? Berechne sowohl mit de Moivre-Laplace und
(ggf. mit Rechnerunterstützung auch mit der Poissonapproximation).
Für die Folge der unabhängigen Zufallsvariablen
![]() gilt
gilt
![]() und
und
![]() .
.
Es gilt
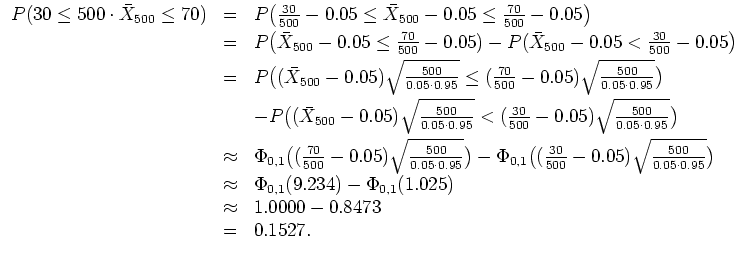
Bei der Poissonapproximation gilt
![]() und es folgt
(mit Rechnerunterstützung)
und es folgt
(mit Rechnerunterstützung)
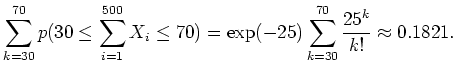
Der genaue Wert ist übrigens
![]() .
.
| automatisch erstellt am 7. 6. 2005 |