Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Verkehrsdichte (linear PDE) zu

Aufgabe 286: Verkehrsdichte, lineare partielle Differentialgleichung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Sei die Verkehrsdichte auf einer Straße durch $ u(x,t)$ gegeben, d.h. $ u(x,t)$ ist die Zahl der Autos an der Stelle $ x$ zum Zeitpunkt $ t$ zwischen $ x$ und $ x + dx$, geteilt durch $ dx$.

Sei der Verkehrsfluß durch $ F(x,t)$ beschrieben. Der Wert $ F(x,t)$ ist hierbei die Zahl der Autos, die die Stelle $ x$ im Zeitraum von $ t$ bis $ t + dt$ in positiver Richtung passieren.

Betrachten wir das Streckenelement $ [x,x+dx]$ zum Zeitpunkt $ t$. Fluß und Dichte hängen über

$\displaystyle (u(x,t+dt) - u(x,t))dx\; =\; - (F(u(x+dx,t)) - F(u(x,t))) dt $

zusammen, da die Änderung der Verkehrsdichte der Zahl der in das Streckenelement bei $ x$ einfahrenden Autos, minus der bei $ x + dx$ ausfahrenden Autos gegeben ist. Also

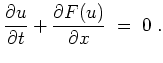
$\displaystyle \frac{\partial u}{\partial t} + \frac{\partial F(u)}{\partial x} \; = \; 0\; . $

(i)
Sei der Verkehrsfluß $ F(x,t)$ nur von $ u$ abhängig - die Geschwindigkeit eines Autos ist durch den Abstand zum Vordermann bestimmt. Wir setzen also $ F(x,t) = F(u(x,t)) = 1 - u$ an. D.h. ist die Verkehrsdichte Null, so fahren alle Autos mit Geschwindigkeit $ 1$, ist die Verkehrsdichte auf $ 1$ angeschwollen, so kommt der Verkehr zum Erliegen. Ist die Verkehrsdichte $ >1$, so kommt es zu Auffahrunfällen.

(ii)
Sei nun der Verkehrfluß noch von der sich den Orten $ x = 2\pi\mathbb{Z}$ befindlichen Polizeistationen abhängig - je näher an $ x = 0$, desto mehr wird auf den zu geringen Abstand zum Vordermann mit Geschwindigkeitsreduktion reagiert. Sei demgemäß $ F(x,t) = F(u(x,t)) = 1 - (1 + a\cos(x)) u$ mit $ a\in [0,1)$.

Gib die allgemeine Lösung der Differentialgleichung in den Fällen (i, ii) an.

Sei nun als Randbedingung $ u(x,0) = 1/2$ vorausgesetzt. Gib die Funktion $ u(x,t)$ in beiden Fällen an.

Fall (i). Zu lösen ist $ \mbox{$u_t - u_x = 0$}$. Als System für die Höhenlinien erhalten wir für einen freien Parameter $ \mbox{$s$}$ das System

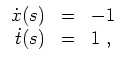
$ \mbox{$\displaystyle \begin{array}{rcl} \dot x(s) & = & -1 \\ \dot t(s) & = & 1\; , \\ \end{array}$}$
woraus wir $ \mbox{$\frac{dx}{dt} = -1$}$ entnehmen. Als Lösung ergibt sich $ \mbox{$x + t = {\mbox{const.}}$}$, so daß die ursprüngliche Gleichung die allgemeine Lösung $ \mbox{$v(x + t)$}$ besitzt.

Fall (ii). Zu lösen ist zunächst die Rumpfdifferentialgleichung $ \mbox{$u_t - (1+a\cos(x)) u_x = 0$}$. Als System für die Höhenlinien erhalten wir für einen freien Parameter $ \mbox{$s$}$ das System

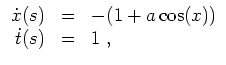
$ \mbox{$\displaystyle \begin{array}{rcl} \dot x(s) & = & -(1+a\cos(x)) \\ \dot t(s) & = & 1\; , \\ \end{array}$}$
woraus wir $ \mbox{$\frac{dx}{dt} = -(1+a\cos(x))$}$ entnehmen, d.h. $ \mbox{$\int dt = - \int (1 + a\cos(x))^{-1} dx$}$. Es wird
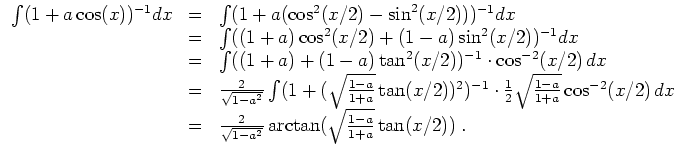
$ \mbox{$\displaystyle \begin{array}{rcl} \int (1 + a\cos(x))^{-1} dx & = & \in... ...{\sqrt{1 - a^2}}\arctan(\sqrt{\frac{1-a}{1+a}}\tan(x/2))\; . \\ \end{array}$}$

Als Lösung ergibt sich 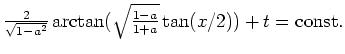$ \mbox{$\frac{2}{\sqrt{1 - a^2}}\arctan(\sqrt{\frac{1-a}{1+a}}\tan(x/2)) + t = {\mbox{const.}}$}$, so daß die Rumpfgleichung die allgemeine Lösung 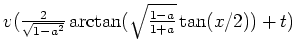$ \mbox{$v(\frac{2}{\sqrt{1 - a^2}}\arctan(\sqrt{\frac{1-a}{1+a}}\tan(x/2)) + t)$}$ besitzt. Für $ \mbox{$a = 0$}$ ergibt sich also tatsächlich die Lösung aus (i) (dort lag ja schon eine Rumpfdifferentialgleichung vor).

Für die Lösung der ursprünglichen Gelichung können wir etwa die Transformation

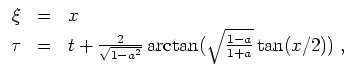
$ \mbox{$\displaystyle \begin{array}{rcl} \xi & = & x \\ \tau & = & t + \frac{2}{\sqrt{1 - a^2}}\arctan(\sqrt{\frac{1-a}{1+a}}\tan(x/2))\; , \\ \end{array}$}$
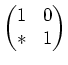verwenden, was wegen Jacobimatrix $ \mbox{$\left(\begin{matrix}1 & 0 \\ \ast & 1\end{matrix}\right)$}$ zulässig ist. Es bleibt
$ \mbox{$\displaystyle -(1 + a\cos(\xi)) \tilde u_\xi + a\sin(\xi)\tilde u \; =\; 0\; . $}$
zu lösen. Es ergibt sich zunächst
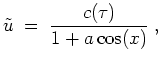
$ \mbox{$\displaystyle \tilde u \; =\; \frac{c(\tau)}{1 + a\cos(x)}\; , $}$
und rücksubstituiert also
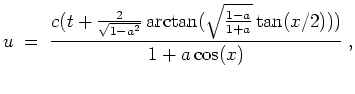
$ \mbox{$\displaystyle u \; =\; \frac{c(t + \frac{2}{\sqrt{1 - a^2}}\arctan(\sqrt{\frac{1-a}{1+a}}\tan(x/2)))}{1 + a\cos(x)}\; , $}$
mit einer beliebigen Funktion $ \mbox{$c$}$.

Nun ist noch das Anfangswertproblem zu lösen.

Im Fall (i) ergibt sich mit $ \mbox{$u(x,0) = v(x) = 1/2$}$, daß $ \mbox{$v$}$ konstant gleich $ \mbox{$1/2$}$ ist, und somit $ \mbox{$u(x,t) = 1/2$}$ gilt. Der Verkehr fließt störungsfrei.

Im Fall (ii) ergibt die Randbedingung

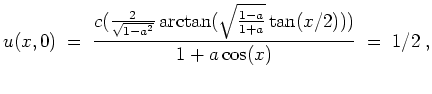
$ \mbox{$\displaystyle u(x,0) \; =\; \frac{c(\frac{2}{\sqrt{1 - a^2}}\arctan(\sqrt{\frac{1-a}{1+a}}\tan(x/2)))}{1 + a\cos(x)} \; =\; 1/2\; , $}$
daß im Ausdruck für $ \mbox{$u(x,t)$}$ auftretende Funktion $ \mbox{$c = c(w)$}$ gegeben ist durch
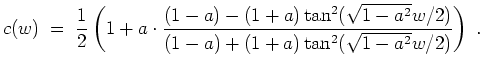
$ \mbox{$\displaystyle c(w)\; =\; \frac{1}{2}\left(1 + a \cdot \frac{(1-a) - (1... ...(\sqrt{1 - a^2} w/2)}{(1-a) + (1 + a)\tan^2(\sqrt{1 - a^2} w/2)}\right) \; . $}$
Hierbei ist $ \mbox{$w$}$ eine Hilfsvariable. Graphisch verläuft für $ \mbox{$a = 0.5$}$ die Verkehrsdichte $ \mbox{$u$}$ in Abhängigkeit von Zeit $ \mbox{$t$}$ und Ort $ \mbox{$x$}$ wie folgt.

\includegraphics[width=10cm]{s2.eps}

Eine gleichmäßige Verkehrsdichte wird gestört.

(Autoren: Künzer/Meister/Nebe)
[Zurück zur Aufgabe]
  automatisch erstellt am 7.  6. 2005