
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 868: Konvergenz von Reihen |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Untersuche jeweils die Reihe
![]() auf Konvergenz. Berechne von wenigstens einer konvergenten Reihe
den Grenzwert.
auf Konvergenz. Berechne von wenigstens einer konvergenten Reihe
den Grenzwert.
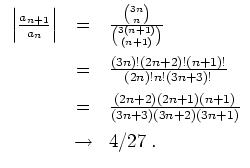
Alternativ kann man auch das Wurzelkriterium gebrauchen. Zunächst bemerken wir, daß aus
der schwachen Stirlingschen Formel
![]() durch Substitution von
durch Substitution von
![]() für
für
![]() und
Potenzieren mit
und
Potenzieren mit
![]() folgt, daß
folgt, daß
![]() . Es wird
. Es wird
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\lim_{n\to\infty} \sqrt[n]{\vert a_n\...
... \cdot \frac{4}{27} \vspace*{2mm}\\
& = & \frac{4}{27}\; . \\
\end{array}$}$](/inhalt/loesung/loesung463/img7.png)
In der Tat ist mit der geometrischen Reihe
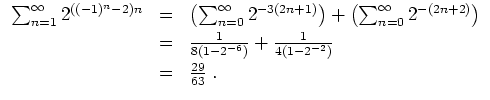
Man kann die Konvergenz der Reihe auch mit dem Majorantenkriterium nachweisen. Es ist nämlich
![]() , und die geometrische Reihe
, und die geometrische Reihe
![]() konvergiert.
konvergiert.
Das Quotientenkriterium versagt hier, da der fragliche Limes superior gleich
![]() , und der fragliche
Limes inferior gleich
, und der fragliche
Limes inferior gleich
![]() ist.
ist.
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\overline {\lim}_{n\to\infty}\sqrt[n]...
...ac{\vert z\vert}{\exp(\alpha(\log n)/n)}\\
&=& \vert z\vert\; .
\end{array}$}$](/inhalt/loesung/loesung463/img16.png)
Im Falle
![]() mit
mit
![]() wollen wir das Dirichletkriterium verwenden mit
wollen wir das Dirichletkriterium verwenden mit
![]() und
und
![]() ,
indem wir zeigen, daß die Partialsummenfolge
,
indem wir zeigen, daß die Partialsummenfolge
![]() beschränkt ist, und daß die Folge
beschränkt ist, und daß die Folge
![]() eine monotone Nullfolge ist.
Es wird
eine monotone Nullfolge ist.
Es wird
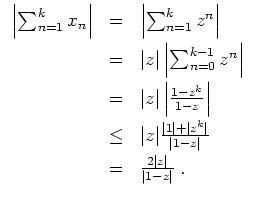
Für
![]() betrachtet man
betrachtet man
![]() . Nach dem Majorantenkriterium folgt aus der Divergenz der harmonischen
Reihe
. Nach dem Majorantenkriterium folgt aus der Divergenz der harmonischen
Reihe
![]() die Divergenz der Reihe
die Divergenz der Reihe
![]() .
.
| automatisch erstellt am 7. 6. 2005 |