Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 881: Eine Ungleichung mittels Integralen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Zeige folgende Abschätzung für $ \mbox{$n\geq 1$}$.

$ \mbox{$\displaystyle n^ne^{1-n} \;\leq\; n! \;\leq\; (n+1)^{n+1/2}e^{-n} \;. $}$

Für die untere Abschätzung betrachte man die Unterteilung $ \mbox{$(1,2,\ldots,n)$}$ des Intervalls $ \mbox{$[1,n]$}$ und die zugehörige Obersumme des Integrals der Logarithmusfunktion. Es wird

$ \mbox{$\displaystyle \begin{array}{rcl} \log(n!) &=& \sum_{k=2}^n  \log k\vsp... ...2mm}\\ &=& [t\log t-t]_1^n\vspace*{2mm}\\ &=& n\log n-n+1 \;. \end{array}$}$
Durch Anwendung der Exponentialfunktion ergibt sich
$ \mbox{$\displaystyle n! \;\geq\; n^n e^{1-n} \; . $}$

Für die obere Abschätzung betrachte man die Unterteilung $ \mbox{$(1,2,\ldots n+1)$}$ des Intervalls $ \mbox{$[1,n+1]$}$ und die zugehörige Untersumme des Integrals der Logarithmusfunktion.

Hierbei lassen sich zwischen dem Graphen der Untersumme und dem Graphen der Logarithmusfunktion noch Dreiecksflächen unterbringen. Wir haben dazu zu überprüfen, daß der Logarithmus oberhalb der Sekanten $ \mbox{$s_k(x)$}$ zwischen den Punkten $ \mbox{$(k,\log k)$}$ und $ \mbox{$(k+1,\log(k+1))$}$ verläuft. Hierzu bestimmen wir das Minimum der Funktion $ \mbox{$\log x-s_k(x)$}$ auf dem Intervall $ \mbox{$[k,k+1]$}$. Wegen $ \mbox{$(\log x-s_k(x))''=-1/x^2<0$}$ ist $ \mbox{$(\log x-s_k(x))'$}$ streng monoton fallend. Mit dem Mittelwertsatz ist bei $ \mbox{$x=k$}$ diese Ableitung positiv, bei $ \mbox{$x=k+1$}$ negativ. Damit gibt es in $ \mbox{$(k,k+1)$}$ genau eine Extremstelle, und diese ist eine Maximalstelle. Folglich nimmt die Funktion $ \mbox{$\log x-s_k(x)$}$ ihr Minimum auf $ \mbox{$[k,k+1]$}$ auf dem Rand $ \mbox{$x=k$}$ bzw. $ \mbox{$x=k+1$}$ an, wo sie den Wert $ \mbox{$0$}$ annimmt. Insbesondere ist $ \mbox{$\log x-s_k(x)\geq 0$}$ für $ \mbox{$x\in[k,k+1]$}$.

Zusammengenommen haben diese Dreiecksflächen den Flächeninhalt $ \mbox{$\log(n+1)/2$}$. Es wird

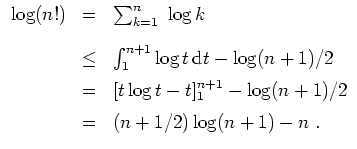
$ \mbox{$\displaystyle \begin{array}{rcl} \log(n!) &=& \sum_{k=1}^n  \log k\vsp... ..._1^{n+1} -\log(n+1)/2\vspace*{2mm}\\ &=& (n+1/2)\log(n+1)-n \;. \end{array}$}$
Durch Anwendung der Exponentialfunktion ergibt sich
$ \mbox{$\displaystyle n! \;\leq\; (n+1)^{n+1/2}e^{-n} \;. $}$

Zum Beispiel wird für $ \mbox{$n = 100$}$

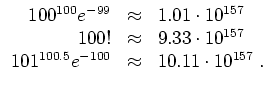
$ \mbox{$\displaystyle \begin{array}{rcl} 100^{100} e^{-99} & \approx & 1.01\c... ...\ 101^{100.5}e^{-100} & \approx & 10.11\cdot 10^{157}\; . \\ \end{array}$}$

Skizze für die obere Abschätzung.

\includegraphics[width=10cm]{s1_log.eps}

(Autoren: Künzer/Martin/Nebe)
[Zurück zur Aufgabe]
  automatisch erstellt am 7.  6. 2005