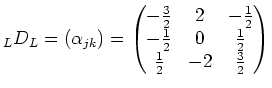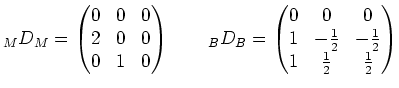Wir betrachten den Polynomraum
Pol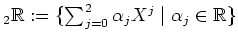 zusammen mit der Abbildung
zusammen mit der Abbildung
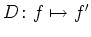 ,
die einem Polynom dessen Ableitung zuordnet.
,
die einem Polynom dessen Ableitung zuordnet.
Bestimmen Sie die Matrixdarstellungen
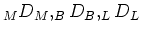 von
von 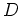 bezüglich
bezüglich
- der Monombasis
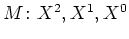 ,
,
- der Basis
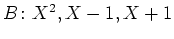 , sowie
, sowie
- der Basis
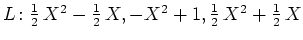 .
.
Um das Verfahren nochmals deutlich zu machen berechnen wir 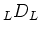 Schritt
für Schritt:
Zunächst müssen wir die Vektoren der Basis
Schritt
für Schritt:
Zunächst müssen wir die Vektoren der Basis 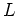 abbilden. Wir erhalten:
abbilden. Wir erhalten:
Nun müssen wir noch die Ergebnisse in Koordinaten bezüglich der Basis 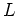 darstellen. Wir müssen
also folgende Gleichungssysteme lösen:
darstellen. Wir müssen
also folgende Gleichungssysteme lösen:
Wir übersetzen dies in Matrizensprache und erhalten:
Achtung, dies ist ein LGS mit mehreren rechten Seiten, die wir simultan lösen.
Die Lösung
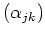 ergibt dann die gesuchte Matrix, also
ergibt dann die gesuchte Matrix, also
Die anderen Matrizen können wir mit demselben Verfahren ausrechnen,
allerdings sind die Rechnungen einfacher. Daher hier nur die Ergebnisse:
(Ackermann/Poppitz)
| |
automatisch erstellt
am 19. 12. 2005 |


![]() zusammen mit der Abbildung
zusammen mit der Abbildung
![]() ,
die einem Polynom dessen Ableitung zuordnet.
,
die einem Polynom dessen Ableitung zuordnet.
![]() von
von ![]() bezüglich
bezüglich
![]() Schritt
für Schritt:
Zunächst müssen wir die Vektoren der Basis
Schritt
für Schritt:
Zunächst müssen wir die Vektoren der Basis ![]() abbilden. Wir erhalten:
abbilden. Wir erhalten:
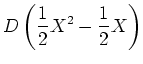
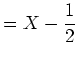
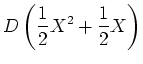
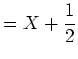
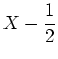
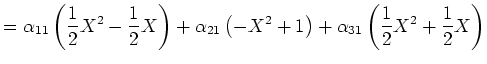
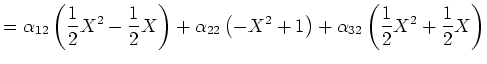
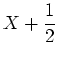
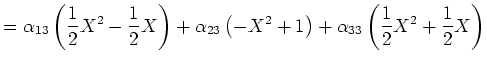
![$\displaystyle \left[\begin{array}{ccc\vert\vert ccc} \frac12 & -1 & \frac12 & 0...
...& \frac12 & 1 & -2 & 1 \\ 0 & 1 & 0 & -\frac12 & 0 & \frac12 \end{array}\right]$](/inhalt/loesung/loesung577/img15.png)