Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Hinweis zu

Aufgabe 1310: Abstands- und Winkelbestimmung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Seien

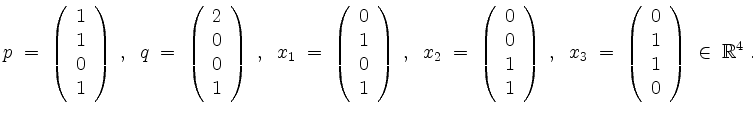
$\displaystyle p \;=\; \left(\begin{array}{r}1\\ 1\\ 0\\ 1\end{array}\right)\;,\... ... \left(\begin{array}{r}0\\ 1\\ 1\\ 0\end{array}\right)\;\in\;\mathbb{R}^4\; . $

Sei $ g$ die Gerade durch $ p$ und $ q$ .

1.
Berechne den Abstand von $ q$ zu $ p + \langle x_1\rangle$ . Berechne den von $ g$ und $ p + \langle x_1\rangle$ eingeschlossenen Winkel.
2.
Berechne den Abstand von $ q$ zu $ p + \langle x_1,x_2\rangle$ . Berechne den von $ g$ und $ p + \langle x_1,x_2\rangle$ eingeschlossenen Winkel.
3.
Berechne den Abstand von $ q$ zu $ p + \langle x_1,x_2,x_3\rangle$ . Berechne den von $ g$ und $ p + \langle x_1,x_2,x_3\rangle$ eingeschlossenen Winkel.

Ergänze $ (x_1,x_2,x_3)$ zu einer Basis des $ \mathbb{R}^4$ und wende Gram-Schmidt an. Die enstandene Orthonormalbasis verwende man, um Hessesche Normalenformen für 1., 2., 3. zu bestimmen, sowie, um die jeweils für die Winkelberechnung benötigte orthogonale Projektion zu erhalten.

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006