Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Hinweis zu

Aufgabe 1314: Eine Determinante

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

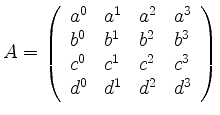Seien $ a,\,b,\,c,\,d\,\in\,\mathbb{R}$ , sei $ A = \left(\begin{array}{llll} a^0 & a^1 & a^2 & a^3 \\ b^0 & b^1 & b^2 & b^3 \\ c^0 & c^1 & c^2 & c^3 \\ d^0 & d^1 & d^2 & d^3 \\ \end{array}\right)$ .

1.
Berechne $ \det A$ . Zeige, daß $ A$ invertierbar ist genau dann, wenn $ a,\,b,\,c,\,d$ paarweise verschieden sind.
2.
Falls $ A$ invertierbar ist, berechne den Eintrag an den Positionen $ (1,3)$ , $ (2,3)$ und $ (3,3)$ von $ A^{-1}$ .

Nach Säubern der ersten Spalte und nachfolgender Laplaceentwicklung ziehe man ein gewisses Vielfaches der zweiten Spalte von der dritten ab, sowie ein gewisses Vielfaches der ersten von der zweiten, ohne daß hierbei notwendigerweise Nullen entstehen. Dann dividiere man in den Zeilen je einen gemeinsamen Faktor ab.

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006