Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1314: Eine Determinante

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

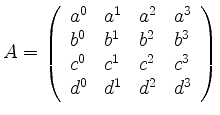Seien $ a,\,b,\,c,\,d\,\in\,\mathbb{R}$ , sei $ A = \left(\begin{array}{llll} a^0 & a^1 & a^2 & a^3 \\ b^0 & b^1 & b^2 & b^3 \\ c^0 & c^1 & c^2 & c^3 \\ d^0 & d^1 & d^2 & d^3 \\ \end{array}\right)$ .

1.
Berechne $ \det A$ . Zeige, daß $ A$ invertierbar ist genau dann, wenn $ a,\,b,\,c,\,d$ paarweise verschieden sind.
2.
Falls $ A$ invertierbar ist, berechne den Eintrag an den Positionen $ (1,3)$ , $ (2,3)$ und $ (3,3)$ von $ A^{-1}$ .

1.
Wir berechnen

\begin{displaymath} \begin{array}{l} \det A \;=\;\det\left(\begin{array}{llll} ... ... (b - a)(c - a)(d - a)(c - b)(d - b)(d - c)\; . \\ \end{array}\end{displaymath}

Dies ist ein Beispiel einer Vandermondeschen Determinanten.

Es folgt aus der Determinante, daß $ A$ genau dann invertierbar ist, wenn $ a$ , $ b$ , $ c$ und $ d$ paarweise verschieden sind.

Hier ist ein alternatives Argument. Sind zwei Elemente aus $ (a,b,c,d)$ gleich, so hat $ A$ zwei gleiche Zeilen und ist singulär.

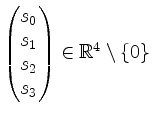Umgekehrt, seien die Einträge in $ (a,b,c,d)$ paarweise verschieden. Angenommen, $ A$ würde den Vektor $ \begin{pmatrix}s_0\\ s_1\\ s_2\\ s_3\end{pmatrix}\in\mathbb{R}^4\setminus\{ 0\}$ annullieren. Dann wäre $ s_0 X^0 + s_1 X^1 + s_2 X^2 + s_3 X^3$ ein nichtverschwindendes Polynom von Grad $ \le 3$ , welches vier verschiedene Nullstellen hat. Das gibt es nicht, und damit ist die Annahme als falsch nachgewiesen. Also ist $ \operatorname{Kern }A = \{0\}$ , und mithin $ A$ regulär.

2.
Mit der Cramerschen Regel berechnen wir zunächst

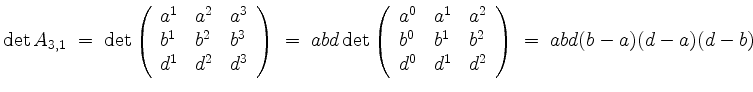
$\displaystyle \det A_{3,1} \;=\; \det \left(\begin{array}{lll} a^1 & a^2 & a^3... ... b^2 \\ d^0 & d^1 & d^2 \\ \end{array}\right) \;=\; abd(b - a)(d - a)(d - b) $

und erhalten den Eintrag

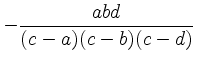
$\displaystyle -\frac{abd}{(c - a)(c - b)(c - d)} $

an Position $ (1,3)$ von $ A^{-1}$ .

Ähnlich berechnen wir

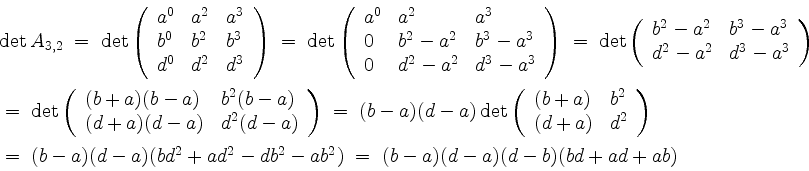
\begin{displaymath} \begin{array}{l} \det A_{3,2} \;=\; \det \left(\begin{array... ... - ab^2) \;=\; (b - a)(d - a)(d - b)(bd + ad + ab) \end{array}\end{displaymath}

und erhalten den Eintrag

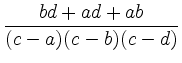
$\displaystyle \frac{bd + ad + ab}{(c - a)(c - b)(c - d)} $

an Position $ (2,3)$ von $ A^{-1}$ .

Schließlich berechnen wir

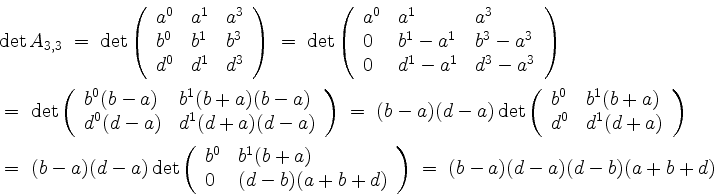
\begin{displaymath} \begin{array}{l} \det A_{3,3} \;=\; \det \left(\begin{array... ...rray}\right) \;=\; (b - a)(d - a)(d - b)(a + b + d) \end{array}\end{displaymath}

und erhalten den Eintrag

$\displaystyle - \frac{a + b + d}{(c - a)(c - b)(c - d)} $

an Position $ (3,3)$ von $ A^{-1}$ .
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 22.  8. 2006