Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1316: Sylvestersche Matrix und Resultante

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Seien $ f(X) = X^3 + aX^2 + bX + 1$ und $ g(X) = X^3 + dX^2 + eX + 1$ reelle Polynome.

1.
Zeige, daß $ f$ und $ g$ genau dann einer Gleichung (Gleichheit von Polynomen) der Form

$\displaystyle (\ast) \hspace*{3cm} u(X)f(X) + v(X)g(X) \;=\; 0 $

für gewisse reellen Polynome $ u(X) = s_2 X^2 + s_1 X^1 + s_0 X^0$ und $ v(X) = t_2 X^2 + t_1 X^1 + t_0 X^0$ , die nicht beide verschwinden sollen, genügen, wenn

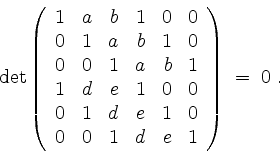
\begin{displaymath} \det\left( \begin{array}{rrrrrr} 1 & a & b & 1 & 0 & 0 \\ ... ... \\ 0 & 0 & 1 & d & e & 1 \\ \end{array}\right) \;=\; 0\; . \end{displaymath}

Diese Matrix heißt auch Sylvestersche Matrix, und ihre Determinante die Resultante der Polynome $ f(X)$ und $ g(X)$ .

2.
Berechne die Resultante von $ f(X)$ und $ g(X)$ .

3.
Zeige, daß die Resultante von $ f(X)$ und $ g(X)$ genau dann verschwindet, wenn ein Polynom $ h(X)$ von Grad $ \geq 1$ existiert, welches $ f(X)$ und $ g(X)$ teilt. Hierbei teile ein Polynom ein anderes, falls ersteres in einer Produktzerlegung letzterens auftritt.

1.
Die Koeffizienten des Polynoms $ u(X)f(X) + v(X)g(X)$ stehen in dem Zeilenvektor, der sich durch Multiplikation des Zeilenvektors $ ({ s_2\;\; s_1\;\; s_0\;\; t_2\; \;t_1\;\; t_0})$ mit der Sylvesterschen Matrix ergibt. Es ist also $ u(X)f(X) + v(X)g(X) = 0$ genau dann nichttrivial lösbar, wenn es einen Zeilenvektor $ ({ s_2\;\; s_1\;\; s_0\;\; t_2\; \;t_1\;\; t_0})$ gibt, der nach Multiplikation mit der Sylvesterschen Matrix verschwindet. Dies ist genau dann der Fall, wenn diese Matrix singulär ist, d.h. wenn ihre Determinante verschwindet.
2.
Wir berechnen

\begin{displaymath} \begin{array}{l} \det\left( \begin{array}{cccccc} 1 & a & b... ... a)^3 - (e - b)^3 + (d - a)(e - b)(ae - bd)\; . \\ \end{array}\end{displaymath}

3.
Ist $ h(X)$ ein gemeinsamer Teiler von $ f(X)$ und $ g(X)$ von Grad $ \geq 1$ , so können wir

$\displaystyle (g(X)/h(X)) f(X) + (-f(X)/h(X)) g(X) \;=\; 0 $

schreiben. Also ist $ (\ast)$ aus 1. erfüllt, und somit verschwindet die Resultante.

Ist umgekehrt $ (\ast)$ aus 1. erfüllt, so haben wir die Existenz eines gemeinsamen Teilers zu zeigen. Jeder irreduzible Faktor von $ f(X)$ ist wegen $ (\ast)$ Faktor von $ v(X)$ oder von $ g(X)$ . Aus Gradgründen kann nun nicht jeder Faktor von $ f(X)$ ein Faktor von $ v(X)$ sein. In anderen Worten, es gibt wenigstens ein Faktor von $ f(X)$ , der auch in $ g(X)$ auftritt.

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006