Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1317: Berechnung der Jordanform

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Sei

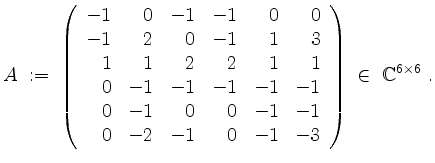
$\displaystyle A\;:=\;\left(\begin{array}{rrrrrr} -1 & 0 & -1 & -1 & 0 & 0 \\ -... ...& -2 & -1 & 0 & -1 & -3 \\ \end{array}\right)\;\in\;\mathbb{C}^{6\times 6}\;. $

1.
Bestimme eine invertierbare Matrix $ S\in\mathbb{C}^{6\times 6}$ so, daß $ J := S^{-1}AS$ in Jordanform ist.
2.
Betrachte die Abbildung

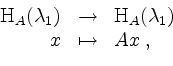
\begin{displaymath} \begin{array}{rcl} \mathrm{H}_A(\lambda_1) &\to & \mathrm{H}_A(\lambda_1)\\ x &\mapsto & Ax\;, \end{array}\end{displaymath}

wobei $ \lambda_1$ der Eigenwert von $ A$ mit algebraischer Vielfachheit vier sei. Bestimme ihre Darstellungsmatrix bezüglich der im Algorithmus mit $ (\underline{y}_1,\ldots,\underline{y}_l)$ bezeichneten Basis.
3.
Berechne $ A^n$ für $ n\geq 0$ .

1.
Das charakteristische Polynom von $ A$ ist

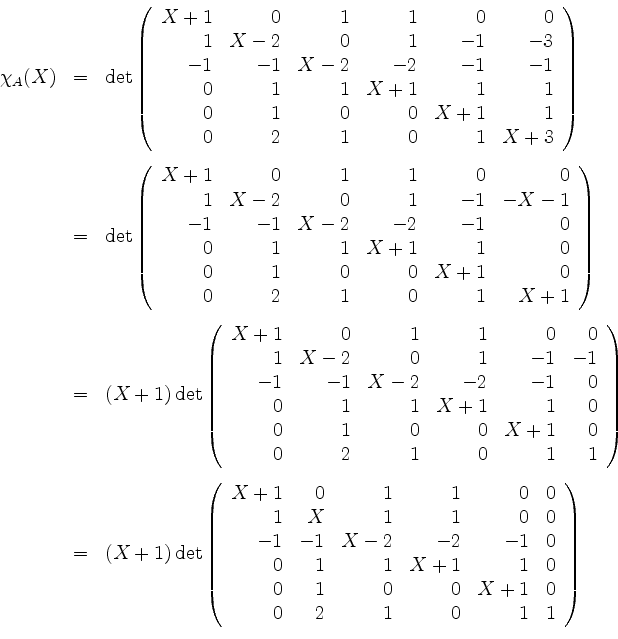
\begin{displaymath} \begin{array}{rcl} \chi_A(X) &=& \det\left(\begin{array}{rrr... ...0 \\ 0 & 2 & 1 & 0 & 1 & 1 \\ \end{array}\right) \end{array}\end{displaymath}

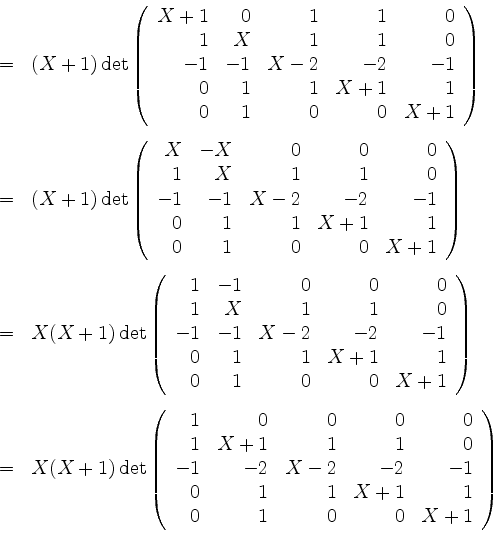
\begin{displaymath} \begin{array}{rcl} &=& (X+1)\det\left(\begin{array}{rrrrr} ... ... \\ 0 & 1 & 0 & 0 & X+1 \\ \end{array}\right)\\ \end{array}\end{displaymath}

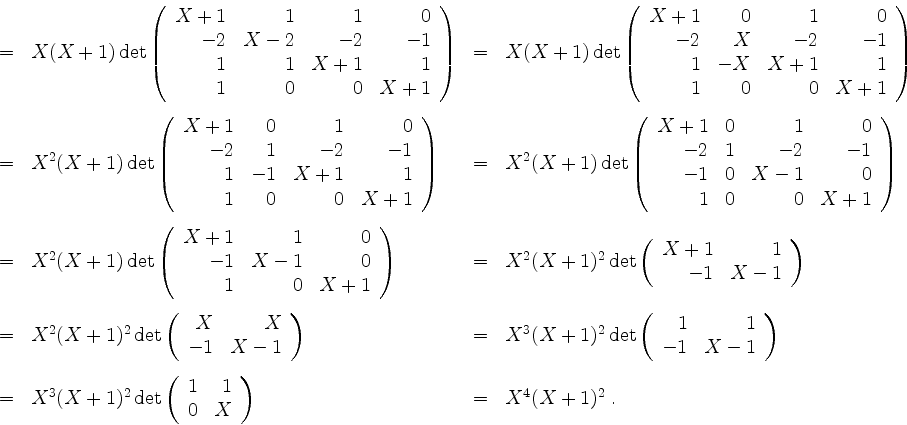
\begin{displaymath} \begin{array}{rclcl} &=& X(X+1)\det\left(\begin{array}{rrrr}... ... X \\ \end{array}\right) \par &=& X^4(X+1)^2\;.\\ \end{array}\end{displaymath}

Die Eigenwerte von $ A$ sind $ \lambda_1=0$ mit algebraischer Vielfachheit vier und $ \lambda_2=-1$ mit algebraischer Vielfachheit zwei.

(Eigenwert $ \lambda_1=0$ )
Wir bringen $ C:=A-\lambda_1\mathrm{E} = A$ auf Zeilenstufenform (inklusive Streichens von Nullzeilen)

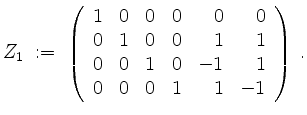
$\displaystyle Z_1 \; :=\; \left(\begin{array}{rrrrrr} 1 & 0 & 0 & 0 & 0 & 0\\ ... ...1\\ 0 & 0 & 1 & 0 & -1 & 1\\ 0 & 0 & 0 & 1 & 1 & -1\\ \end{array}\right)\;. $

Wir erhalten als Basis von $ \operatorname{Kern }C = \operatorname{Kern }Z_1$

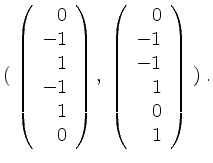
$\displaystyle (\; \left(\begin{array}{r}0\\ -1\\ 1\\ -1\\ 1\\ 0\end{array}\right),\; \left(\begin{array}{r}0\\ -1\\ -1\\ 1\\ 0\\ 1\end{array}\right) \;) \; . $

Nun bringen wir $ Z_1 C$ auf Zeilenstufenform

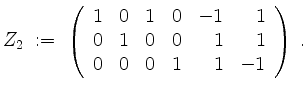
$\displaystyle Z_2 \; :=\; \left(\begin{array}{rrrrrr} 1 & 0 & 1 & 0 & -1 & 1\\ 0 & 1 & 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 1 & 1 & -1\\ \end{array}\right)\;. $

Position $ 3$ ist eine neu hinzugekommene nichtausgewählte Spaltenposition. Wir können also die Basis von $ \operatorname{Kern }C$ ergänzen zu einer Basis von $ \operatorname{Kern }C^2 = \operatorname{Kern }Z_2$

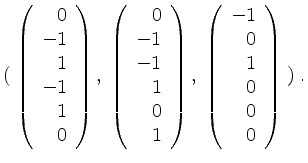
$\displaystyle (\; \left(\begin{array}{r}0\\ -1\\ 1\\ -1\\ 1\\ 0\end{array}\righ... ...ht),\; \left(\begin{array}{r}-1\\ 0\\ 1\\ 0\\ 0\\ 0\end{array}\right) \;) \; . $

Nun bringen wir $ Z_2 C$ auf Zeilenstufenform

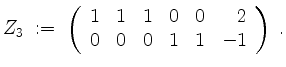
$\displaystyle Z_3 \; :=\; \left(\begin{array}{rrrrrr} 1 & 1 & 1 & 0 & 0 & 2 \\ 0 & 0 & 0 & 1 & 1 & -1 \\ \end{array}\right)\;. $

Position $ 2$ ist eine neu hinzugekommene nichtausgewählte Spaltenposition. Wir können also die Basis von $ \operatorname{Kern}(C^2)$ ergänzen zu einer Basis von $ \operatorname{Kern }C^3 = \operatorname{Kern }Z_3$

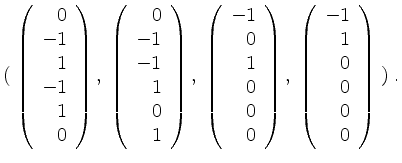
$\displaystyle (\; \left(\begin{array}{r}0\\ -1\\ 1\\ -1\\ 1\\ 0\end{array}\righ... ...ht),\; \left(\begin{array}{r}-1\\ 1\\ 0\\ 0\\ 0\\ 0\end{array}\right) \;) \; . $

Nun ist $ \operatorname{Kern }C^3 = \mathrm{H}_A(0)$ , da seine Dimension gleich der algebraischen Vielfachheit von 0 als Eigenwert von $ A$ ist, nämlich gleich $ 4$ .

Das Tableau zu $ \mathrm{H}_A(\lambda_1)$ sieht also vor der Kettenbildung wie folgt aus.

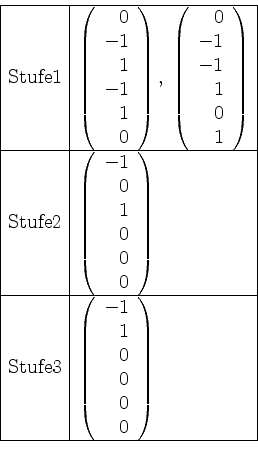
\begin{displaymath} \begin{array}{\vert l\vert l\vert}\hline \mathrm{Stufe }1 & ... ...r}-1\\ 1\\ 0\\ 0\\ 0\\ 0\end{array}\right)\\ \hline \end{array}\end{displaymath}

Nun bilden wir den Vektor in Stufe $ 3$ mittels $ C$ ab, tragen ihn in Stufe $ 2$ ein, und streichen den bereits vorhanden Vektor in Stufe $ 2$ aus Dimensionsgründen.

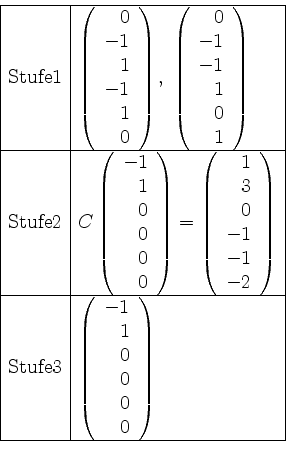
\begin{displaymath} \begin{array}{\vert l\vert l\vert}\hline \mathrm{Stufe }1 & ... ...\\ 1\\ 0\\ 0\\ \,\!0\\ 0\end{array}\right)\\ \hline \end{array}\end{displaymath}

Nun bilden wir den Vektor in Stufe $ 2$ mittels $ C$ ab, tragen ihn in Stufe $ 1$ ein, und streichen den zweiten der schon vorhandenen Vektoren in Stufe $ 1$ (der zufälligerweise mit dem neu eingetragenen Vektor identisch ist). Abschließend sieht unser Tableau also wie folgt aus.

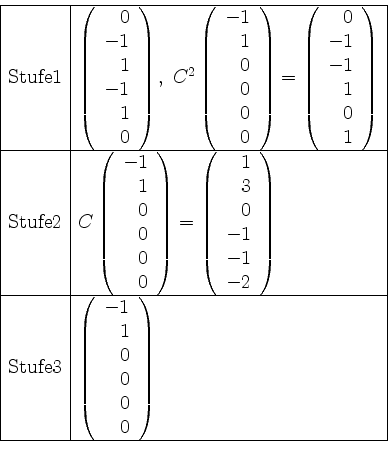
\begin{displaymath} \begin{array}{\vert l\vert l\vert}\hline \mathrm{Stufe }1 & ... ...\\ 1\\ 0\\ 0\\ 0\\ \,\!0\end{array}\right)\\ \hline \end{array}\end{displaymath}

(Eigenwert $ \lambda_2=-1$ )
Wir bringen $ C:=A-\lambda_2\mathrm{E} = A + \mathrm{E}$ auf Zeilenstufenform

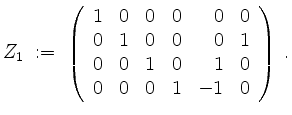
$\displaystyle Z_1 \; :=\; \left(\begin{array}{rrrrrr} 1 & 0 & 0 & 0 & 0 & 0 \\ ... ... \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & -1 & 0\\ \end{array}\right)\;. $

Wir erhalten als Basis von $ \operatorname{Kern }C = \operatorname{Kern }Z_1$

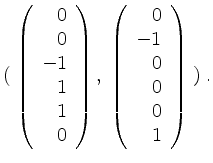
$\displaystyle (\; \left(\begin{array}{r}0\\ 0\\ -1\\ 1\\ 1\\ 0\end{array}\right),\; \left(\begin{array}{r}0\\ -1\\ 0\\ 0\\ 0\\ 1\end{array}\right) \;) \; . $

Nun ist $ \mathrm{E}_A(-1) = \operatorname{Kern }C^1 = \mathrm{H}_A(-1)$ , da seine Dimension gleich der algebraischen Vielfachheit von $ -1$ als Eigenwert von $ A$ ist, nämlich gleich $ 2$ .

Das Tabelau zum Hauptraum $ \mathrm{H}_A(\lambda_2)$ sieht also wie folgt aus.

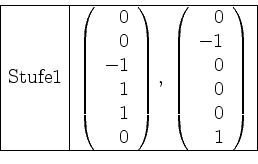
\begin{displaymath} \begin{array}{\vert l\vert l\vert}\hline \mathrm{Stufe }1 & ... ...}0\\ -1\\ 0\\ 0\\ 0\\ 1\end{array}\right) \\ \hline \end{array}\end{displaymath}

Der zweite Schritt, die Kettenbildung, entfällt hier.

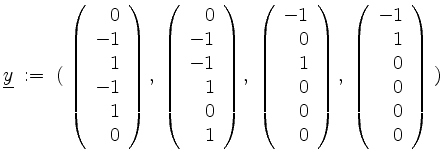
Zusammensetzen der Bestandteile liefert die Kettenbasis von $ \mathbb{C}^6$ , und somit

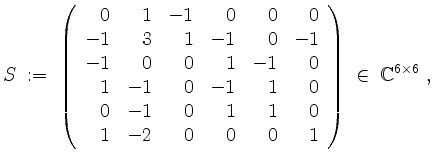
$\displaystyle S\;:=\;\left(\begin{array}{rrrrrr} 0 & 1 & -1 & 0 & 0 & 0 \\ -1 ... ... 1 & -2 & 0 & 0 & 0 & 1 \\ \end{array}\right)\;\in\;\mathbb{C}^{6\times 6}\;, $

sowie

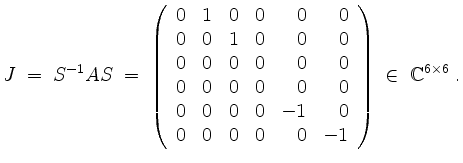
$\displaystyle J \;=\; S^{-1}AS \;=\; \left(\begin{array}{rrrrrr} 0 & 1 & 0 & 0 ... ...0 & 0 & 0 & 0 & 0 & -1 \\ \end{array}\right)\;\in\;\mathbb{C}^{6\times 6}\; . $

Anstatt $ S^{-1}AS$ als Produkt tatsächlich auszurechnen, rechnen wir die Probe $ AS = SJ$ . Zusammen mit einer direkten Überprüfung der Invertierbarkeit von $ S$ haben wir eine sichere Probe des Resultates durchgeführt.

2.
Bezüglich der Basis

$\displaystyle \underline{y} \; :=\; (\; \left(\begin{array}{r}0\\ -1\\ 1\\ -1\\... ...}\right),\; \left(\begin{array}{r}-1\\ 1\\ 0\\ 0\\ 0\\ 0\end{array}\right) \;) $

von $ \mathrm{H}_A(0)$ erhalten wir

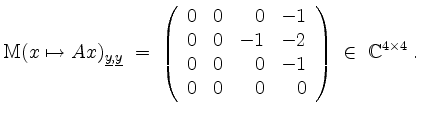
$\displaystyle \mathrm{M}(x\mapsto Ax)_{\underline{y},\underline{y}} \;=\; \lef... ...& -1 \\ 0 & 0 & 0 & 0 \\ \end{array}\right)\;\in\;\mathbb{C}^{4\times 4}\; . $

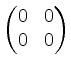Dies ist eine obere Blockdreiecksmatrix mit Hauptdiagonalblöcken $ \begin{pmatrix}0&0\\ 0&0\end{pmatrix}$ , $ \left(0\right)$ , $ \left(0\right)$ . Warum?

3.
Gesondert führen wir $ A^0 = E$ , $ A^1 = A$ und

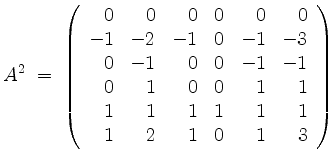
$\displaystyle A^2 \;=\; \left(\begin{array}{rrrrrr} 0 & 0 & 0 & 0 & 0 & 0 \\ -... ...& 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 2 & 1 & 0 & 1 & 3 \\ \end{array}\right) $

an. Denn es ist $ J^n = \mathrm{diag}(0,0,0,0,(-1)^n,(-1)^n)$ für $ n\geq 3$ , und somit erhalten wir mit der nun doch zu berechnenden Inversen

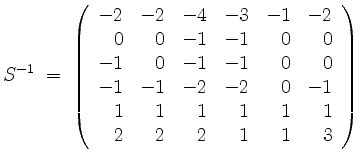
$\displaystyle S^{-1} \;=\; \left(\begin{array}{rrrrrr} -2 & -2 & -4 & -3 & -1 &... ... -1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 2 & 2 & 2 & 1 & 1 & 3 \\ \end{array}\right) $

das Resultat

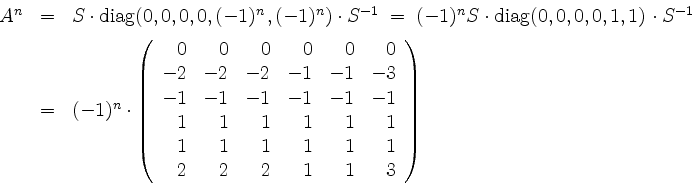
\begin{displaymath} \begin{array}{rcl} A^n &=& S \cdot\mathrm{diag}(0,0,0,0,(-1... ...1 \\ 2 & 2 & 2 & 1 & 1 & 3 \\ \end{array}\right) \end{array}\end{displaymath}

für $ n\geq 3$ .
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 22.  8. 2006