
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1319: Berechnung der Jordanform |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Sei

Bestimme eine invertierbare Matrix
Es wird
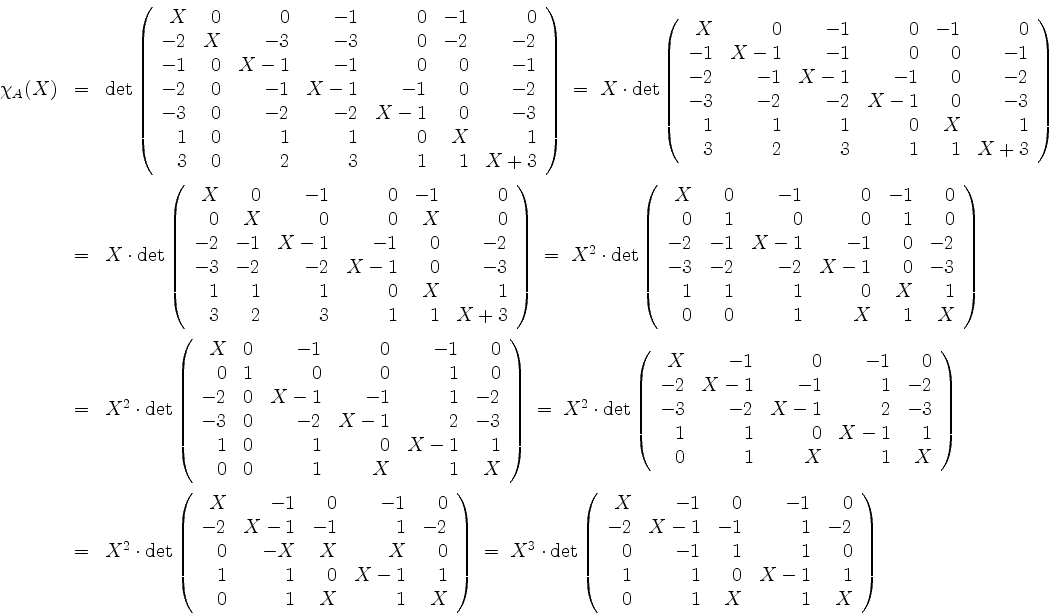
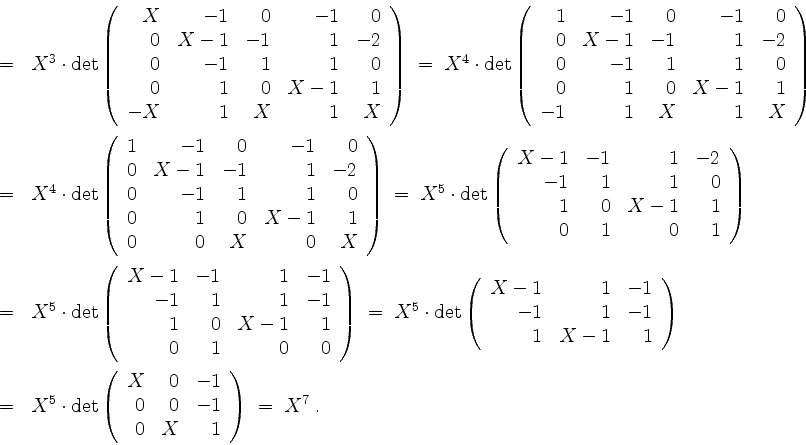
Dies liefert einen Eigenwert 0 mit der algebraischen Vielfachheit eins.
Wenden wir den Algorithmus in formaler Schreibweise an. Es ist ![]() .
.
Mit der Zeilenstufenform

von
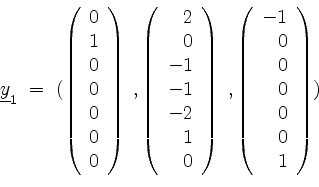
als eine Basis von
Mit der Zeilenstufenform
von
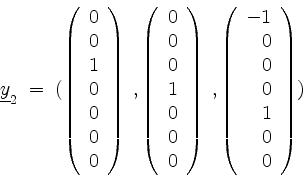
als eine Basisergänzung von
Nun ist
![]() . Damit erhalten wir
. Damit erhalten wir
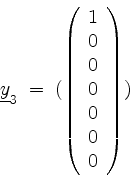
als eine Basisergänzung von
In Stufe ![]() nehmen wir
nehmen wir
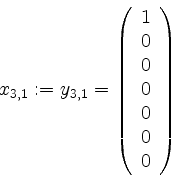 .
.
In Stufe ![]() ist zunächst
ist zunächst
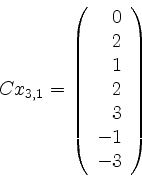 .
.
Da wir nun auf Augenschein hin keine Auswahl mehr treffen können, formen wir nun die Matrix
![]() in die Zeilenstufenform
in die Zeilenstufenform
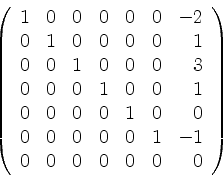
Da hierin die letzte Spaltenposition nichtausgewählt ist, können unter Weglassen des letzten Vektors die Basis
(Man hätte auch ![]() streichen können, nicht aber
streichen können, nicht aber ![]() , wie man dieser Zeilenstufenform ansehen kann.)
, wie man dieser Zeilenstufenform ansehen kann.)
In Stufe ![]() erhalten wir die Basis
erhalten wir die Basis
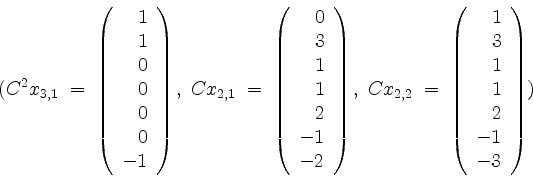
von
Wir setzen die Ketten
![]() ,
,
![]() ,
,
![]() in die Matrix
in die Matrix
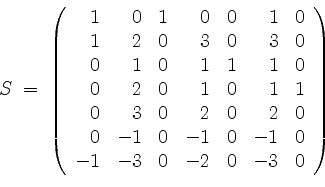
und erhalten
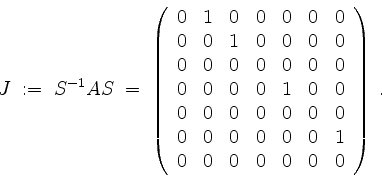
Zur Probe verifizieren wir noch, daß
| automatisch erstellt am 11. 8. 2006 |