
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1324: Jacobimatrix von Koordinatentransformationen und ihre Determinante |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Berechne alle partiellen Ableitungen erster und zweiter Ordnung von ![]() . Zeige, daß im Punkt
. Zeige, daß im Punkt
![]() folgendes gilt.
folgendes gilt.
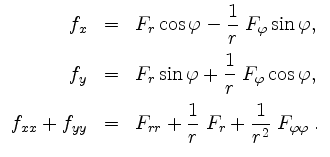
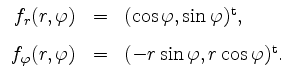
Die partiellen Ableitungen sind als Komposition stetiger Funktionen stetig, und damit ist insbesondere
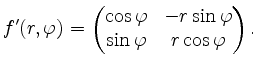
Die Determinante der Jacobimatrix ergibt sich zu
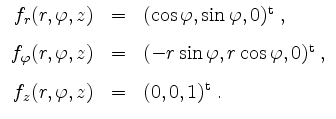
Die partiellen Ableitungen sind als Komposition stetiger Funktionen stetig, und daher ist
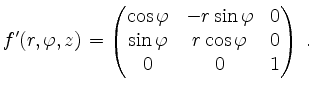
Mittels Laplace-Entwicklung und Aufgabenteil (a) erhalten wir
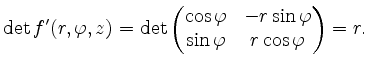
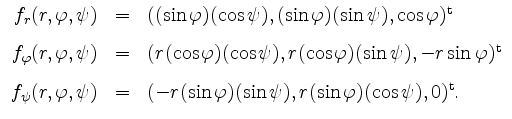
Die partiellen Ableitungen sind als Komposition stetiger Funktionen stetig, und demzufolge ist
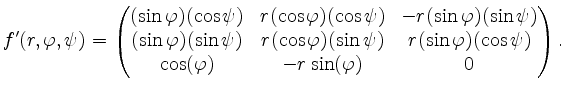
Wir berechnen die Determinante von
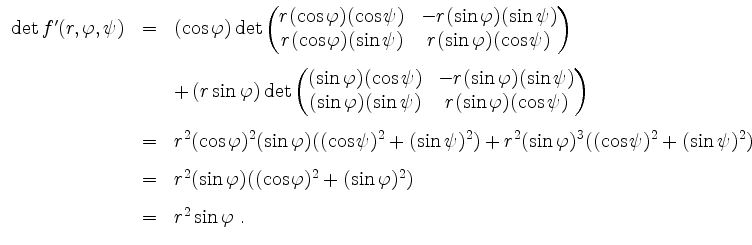
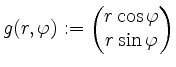 .
Wir berechnen die Ableitung von
.
Wir berechnen die Ableitung von
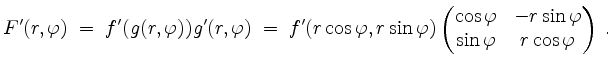
Diese Gleichung können wir nach
![]() auflösen,
indem wir mit der inversen Matrix von rechts multiplizieren. Es wird
auflösen,
indem wir mit der inversen Matrix von rechts multiplizieren. Es wird
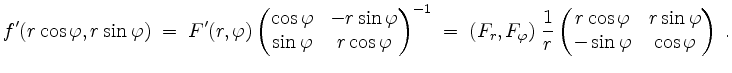
Daraus ergibt sich
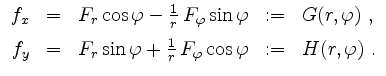
Verwendet man dieses Ergebnis für
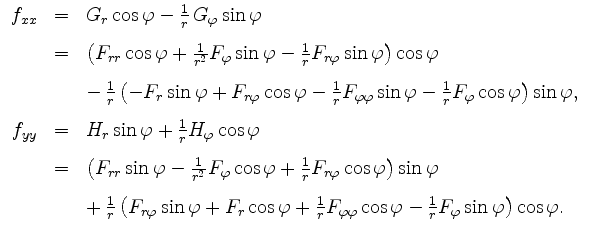
Es folgt also letztendlich
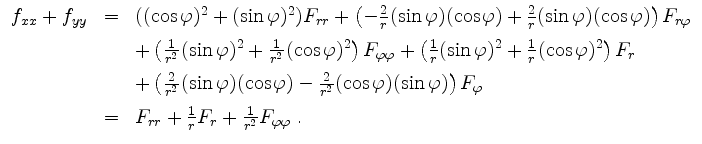
| automatisch erstellt am 11. 8. 2006 |