Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1331: Extrema auf der abgeschlossenen Kreisscheibe

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Bestimmen Sie die globalen Extrema der Funktion

$\displaystyle f(x,y)=e^{x(y+1)} $

auf der Einheitskreisscheibe $ x^2+y^2\leq 1$ .

Zunächst untersuchen wir die Funktion auf lokale Extrema auf der offenen Menge $ \{(x,y)^\mathrm{t}\in\mathbb{R}^2\,\vert\,x^2+y^2 < 1\}$ .

Die notwendige Bedingung

$\displaystyle f'(x,y) \;=\; ((y+1)e^{x(y+1)}, x e^{x(y+1)}) \;\overset{\!}{=}\; 0 $

liefert

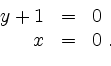
\begin{displaymath} \begin{array}{rcl} y+1 & = & 0\\ x & = & 0\; . \end{array}\end{displaymath}

Der einzige kritische Punkt ist somit der Punkt $ (0,-1)^\mathrm{t}$ , der aber nicht in der Menge $ \{(x,y)^\mathrm{t}\in\mathbb{R}^2\,\vert\,x^2+y^2 < 1\}$ liegt.

Also gibt es auf $ \{(x,y)^\mathrm{t}\in\mathbb{R}^2\,\vert\,x^2+y^2 < 1\}$ kein lokales Extremum. Eine globale Extremstelle auf der gesamten Menge $ \{(x,y)^\mathrm{t}\in\mathbb{R}^2\,\vert\,x^2+y^2 \leq 1\}$ , welche in $ \{(x,y)^\mathrm{t}\in\mathbb{R}^2\,\vert\,x^2+y^2 < 1\}$ liegt, wäre aber insbesondere eine solche lokale Extremstelle. Damit gibt es auf $ \{(x,y)^\mathrm{t}\in\mathbb{R}^2\,\vert\,x^2+y^2 < 1\}$ auch kein globales Extremum.

Da die Menge $ \{(x,y)^\mathrm{t}\in\mathbb{R}^2\,\vert\,x^2+y^2\le 1\}$ kompakt ist, und da $ f$ stetig ist, existieren dort sowohl globales Maximum als auch globales Minimum. Nach dem obigen Resultat werden beide auf dem Rand $ \{(x,y)^\mathrm{t}\in\mathbb{R}^2\,\vert\,x^2+y^2=1\}$ angenommen.

Die Nebenbedingung lautet mit $ g(x,y) := x^2+y^2-1$ also $ g(x,y) = 0$ . Sei

$\displaystyle F(x,y)\; :=\; f(x,y) - \lambda g(x,y) \; . $

Wir wollen die Multiplikatorenregel von Lagrange verwenden. Die dabei notwendige Voraussetzung

$\displaystyle \mathrm{Rang} g'(x,y) \;=\; \mathrm{Rang} (2x,2y) \;\overset{\!}{=}\; 1 $

ist erfüllt für alle $ (x,y)^\mathrm{t}\in\mathbb{R}^2$ mit $ g(x,y) = 0$ .

Wir bestimmen nun alle regulären kritischen Punkte unter Nebenbedingung $ g = 0$ vermittels

$\displaystyle F'(x,y)\;=\;((y+1)e^{x(y+1)},xe^{x(y+1)})^\mathrm{t} - \lambda (2x,2y)^\mathrm{t} \;\overset{\!}{=}\; 0\; , $

d.h. vermittels

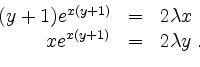
\begin{displaymath} \begin{array}{rcl} (y+1)e^{x(y+1)} & = & 2\lambda x\\ xe^{x(y+1)} & = & 2\lambda y \; . \\ \end{array}\end{displaymath}

Im Falle $ x=0$ folgt aus der Nebenbedingung $ y=\pm 1$ , und somit $ \lambda = 0$ . Nun gibt $ y= +1$ einen Widerspruch. Dagegen ist $ (0,-1)^\mathrm{t}$ in der Tat ein kritischer Punkt.

Im Falle $ y=0$ ist gemäß der Nebenbedingung $ x=\pm 1$ , im Widerspruch zur obigen Gleichung.

Daher können wir uns von nun an auf den Fall $ x\ne 0$ und $ y\ne 0$ konzentrieren. Es ergibt sich

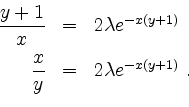
\begin{displaymath} \begin{array}{rcl} \dfrac{y+1}{x} & = & 2\lambda e^{-x(y+1)}... ...\\ \dfrac{x}{y} & = & 2\lambda e^{-x(y+1)}\; . \\ \end{array}\end{displaymath}

Gleichsetzen der linken Seiten gibt 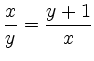$ \dfrac{x}{y} = \dfrac{y+1}{x}$ , d.h. $ x^2 = y^2 + y$ . Unter Verwendung der Nebenbedingung $ x^2+y^2=1$ ergibt sich

$\displaystyle 2y^2+y-1\;=\; 0 \; , $

und hieraus $ y\in\{ -1, 1/2 \}$ . Insgesamt haben wir also die kritischen Punkte

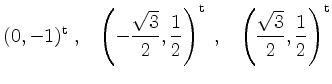
$\displaystyle (0,-1)^\mathrm{t}\;,\;\;\; \left(-\dfrac{\sqrt 3}{2},\dfrac{1}{2}... ...^\mathrm{t}\; ,\;\;\; \left(\dfrac{\sqrt 3}{2},\dfrac{1}{2}\right)^\mathrm{t} $

für lokale Extremstellen unter der Nebenbedingung $ g = 0$ .

Wir vergleichen die Funktionswerte

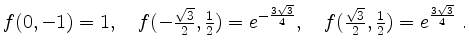
$\displaystyle f(0,-1)=1,\quad f(-\tfrac{\sqrt 3}{2},\tfrac{1}{2})=e^{-\frac{3\sqrt 3}{4}}, \quad f(\tfrac{\sqrt 3}{2},\tfrac{1}{2})=e^{\frac{3\sqrt 3}{4}}\; . $

Also hat $ f$ unter der Nebenbedingung $ g = 0$ ein globales Maximum an der Stelle $ (\frac{\sqrt 3}{2},\frac{1}{2})^\mathrm{t}$ mit dem Funktionswert $ e^{\frac{3\sqrt 3}{4}}$ und ein globales Minimum an der Stelle $ (-\frac{\sqrt 3}{2},\frac{1}{2})^\mathrm{t}$ mit dem Funktionswert $ e^{-\frac{3\sqrt 3}{4}}$ .

Wie bereits oben ausgeführt, sind dies auch die globalen Extrema von $ f$ auf der Menge $ \{(x,y)^\mathrm{t}\in\mathbb{R}^2 :x^2+y^2\leq 1\}$ .

Untersuchen wir unsere kritischen Punkte interessehalber auch noch auf lokale Extrema unter Nebenbedingung $ g = 0$ . Natürlich wissen wir bereits, daß die beiden globalen Extrema auch lokale Extrema zu sein haben. Mit etwas Glück - unsere diesbezügliche Bedingung ist zwar hinreichend, nicht aber notwendig - sollte sich das auch bestätigen.

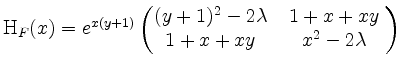Für beliebiges $ \lambda$ und beliebiges $ x$ wird $ \mathrm{H}_F(x) = e^{x(y+1)}\begin{pmatrix}(y+1)^2-2\lambda&\; 1 + x + xy\;\\ \; 1 + x + xy\;&x^2-2\lambda\end{pmatrix}$ .

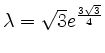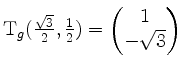Bei $ (\frac{\sqrt 3}{2},\frac{1}{2})^\mathrm{t}$ ist $ \lambda = \sqrt{3} e^{\frac{3\sqrt 3}{4}}$ , es ist $ g'(\frac{\sqrt 3}{2},\frac{1}{2}) = (\sqrt{3}, 1)$ , und wir können $ \mathrm{T}_g(\frac{\sqrt 3}{2},\frac{1}{2}) = \begin{pmatrix}1\\ -\sqrt{3}\end{pmatrix}$ nehmen. Die relative Hessematrix ergibt sich zu

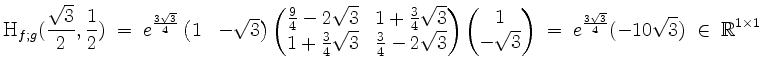
$\displaystyle \mathrm{H}_{f;g}(\frac{\sqrt 3}{2},\frac{1}{2}) \;=\; e^{\frac{3... ...rix}\;=\; e^{\frac{3\sqrt 3}{4}} (- 10\sqrt{3})\; \in\; \mathbb{R}^{1\times 1} $

und ist negativ definit. In der Tat liegt also bei $ (\frac{\sqrt 3}{2},\frac{1}{2})^\mathrm{t}$ ein lokales Maximum vor.

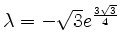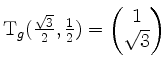Bei $ (-\frac{\sqrt 3}{2},\frac{1}{2})^\mathrm{t}$ ist $ \lambda = -\sqrt{3} e^{\frac{3\sqrt 3}{4}}$ , es ist $ g'(-\frac{\sqrt 3}{2},\frac{1}{2}) = (-\sqrt{3}, 1)$ , und wir können $ \mathrm{T}_g(\frac{\sqrt 3}{2},\frac{1}{2}) = \begin{pmatrix}1\\ \sqrt{3}\end{pmatrix}$ nehmen. Die relative Hessematrix ergibt sich zu

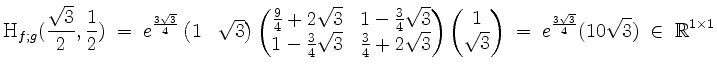
$\displaystyle \mathrm{H}_{f;g}(\frac{\sqrt 3}{2},\frac{1}{2}) \;=\; e^{\frac{3... ...atrix}\;=\; e^{\frac{3\sqrt 3}{4}} (10\sqrt{3})\; \in\; \mathbb{R}^{1\times 1} $

und ist positiv definit. In der Tat liegt also bei $ (-\frac{\sqrt 3}{2},\frac{1}{2})^\mathrm{t}$ ein lokales Minimum vor.

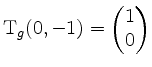Bei $ (0,-1)$ ist $ \lambda = 0$ , es ist $ g'(0,-1) = (0, -2)$ , und wir können $ \mathrm{T}_g(0,-1) = \begin{pmatrix}1 \\ 0\end{pmatrix}$ nehmen. Die relative Hessematrix ergibt sich zu

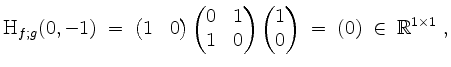
$\displaystyle \mathrm{H}_{f;g}(0,-1) \;=\; \begin{pmatrix}1 & 0\end{pmatrix}\b... ...\begin{pmatrix}1 \\ 0\end{pmatrix}\;=\; (0)\; \in\; \mathbb{R}^{1\times 1}\; , $

und wir können im einzigen noch offengebliebenen Fall keine Entscheidung über ein lokales Extremum unter Nebenbedingung $ g = 0$ treffen.

Skizze von $ f$ auf $ \{(x,y)^\mathrm{t}\in\mathbb{R}^2\,\vert\,x^2+y^2\le 1\}$ .

\includegraphics[width = 8cm]{s3.eps}
(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Zurück zur Aufgabe]
  automatisch erstellt am 11.  8. 2006