
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1338: Kurvenintegral |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
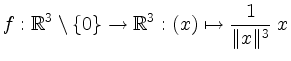
das Kurvenintegral über das sogenannte Vivianische Fenster
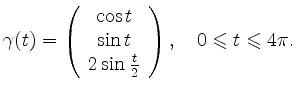
Wir geben drei Lösungsmöglichkeiten an.

Also ist

Aus Symmetriegründen ist daher auch

Also erfüllt
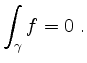
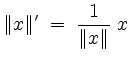
für
Speziell gilt also mit
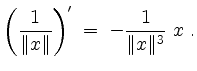
Also ist die Funktion
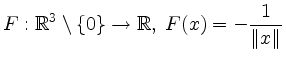
eine Stammfunktion von
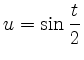 und
und
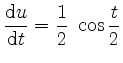

Skizze des Vivianischen Fensters.
![\includegraphics[width = 8cm]{s2.eps}](/inhalt/loesung/loesung698/img20.png)
| automatisch erstellt am 11. 8. 2006 |