
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1360: Fouriertransformation, Faltung, Poissonsche Summenformel, Parsevalsche Gleichung |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Sei
![]() .
.
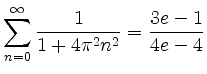 .
.
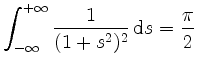 .
.

Aus Symmetriegründen wird also
für


Nun ist aber auch

Ein Vergleich ergibt
![$\displaystyle [\vert t\vert e^{-\vert t\vert}]^\wedge(\omega) \; =\; \dfrac{2(1 - \omega^2)}{(1+\omega^2)^2}
$](/inhalt/loesung/loesung742/img8.png)
für

Die rechte Seite liefert

Ein Vergleich ergibt

wie behauptet.

Die rechte Seite wird zu

Ein Vergleich liefert

wie behauptet.
Das Ergebnis in (5) ergibt sich auch aus dem Residuensatz, denn
![]() ist in der oberen Halbebene
ist in der oberen Halbebene
![]() betragsmäßig hinreichend klein für
betragsgroße
betragsmäßig hinreichend klein für
betragsgroße ![]() , und hat dort nur bei
, und hat dort nur bei
![]() einen Pol, und zwar von Ordnung
einen Pol, und zwar von Ordnung ![]() und mit Residuum
und mit Residuum
![]() . Als Integralwert erhalten wir somit
. Als Integralwert erhalten wir somit
![]() , was unser Ergebnis
bestätigt.
, was unser Ergebnis
bestätigt.
| automatisch erstellt am 11. 8. 2006 |