
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1368: Ein System von linearen Differentialgleichungen zweiter Ordnung |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Löse das System
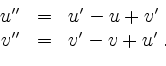
Es ist
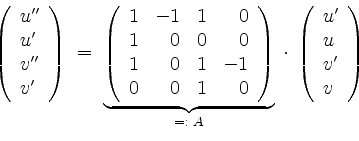
zu lösen.
Berechnen wir die Jordanform von ![]() . Zunächst wird
. Zunächst wird
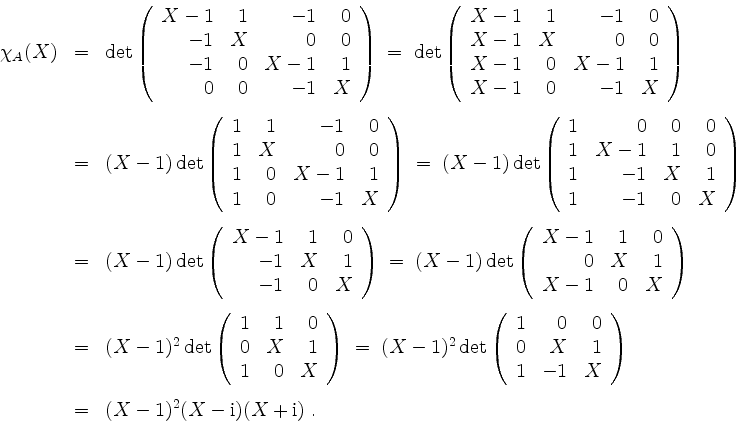
Es ist
 ein Eigenvektor zum Eigenwert
ein Eigenvektor zum Eigenwert
![]() , und
, und
 ein Eigenvektor zum Eigenwert
ein Eigenvektor zum Eigenwert
![]() .
.
Beim Eigenwert ![]() berechnen wir eine Zeilenstufenform
berechnen wir eine Zeilenstufenform
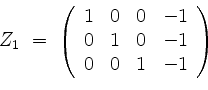
von
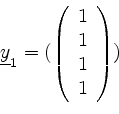 von
von
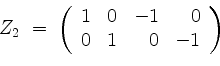
von
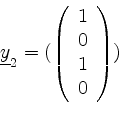 von
von
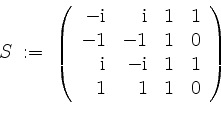
die Jordanform
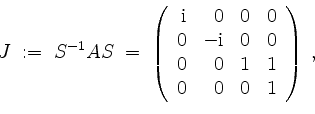
und somit
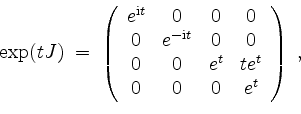
was uns zu der ein Fundamentalsystem in ihren Spalten beinhaltenden Matrix
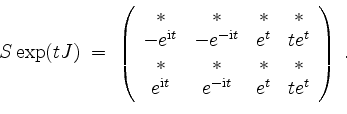
Die mit
Wir erhalten als allgemeine Lösung
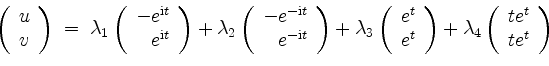
mit
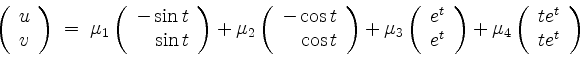
mit
Alternativ kann man auch ![]() und
und
![]() setzen, und das System
setzen, und das System
![]() ,
,
![]() lösen. Ein solcher Trick ist allerdings selten anwendbar.
lösen. Ein solcher Trick ist allerdings selten anwendbar.
| automatisch erstellt am 22. 8. 2006 |