Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1535: Interpolation von Geländedaten

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Aus den an den Punkten $ x_k=(x_{k,1},x_{k,2})\in[0,1]^2$ gemessenen Höhen $ f_k$ soll ein Geländeprofil $ p$ mit Hilfe der Approximation

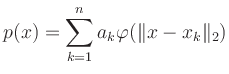
$\displaystyle p(x) = \sum_{k=1}^{n} a_k \varphi(\Vert x-x_k\Vert _2) $

rekonstruiert werden. Schreiben Sie ein Programm a=landscape(x,f), das die Koeffizienten $ a$ für die Basisfunktion $ \varphi(t) = (1 + t^2)^{-1}$ durch Interpolation bestimmt.
Um das Geländeprofil $ p$ zu bestimmen, stellt man folgende Gleichungen auf, welche die Interpolation an den Datenpunkten beschreiben:

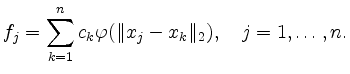
$\displaystyle f_j = \sum_{k=1}^n c_k\varphi(\Vert x_j-x_k\Vert _2),\quad j=1,\ldots,n. $

Dies führt auf das lineare Gleichungssystem

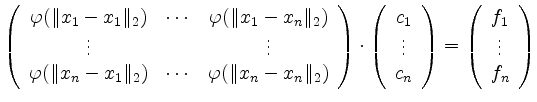
$\displaystyle \left( \begin{array}{ccc}\varphi(\Vert x_1-x_1\Vert _2) & \cdots ... ...} \right) = \left( \begin{array}{c} f_1 \\ \vdots \\ f_n \end{array} \right) $

Damit lautet das MATLAB-File zur Berechnung der Koeffizienten $ a_k$ : 
function a = landscape(x,f);
% function a = landscape(x,f);
%
% input:  x...2xn Punkte
%         f...1xn Funktionswerte an den Punkten
% output: a...1xn Koeffizienten fuer die Basisfunktion 

n = length(f);
U = x(1,:)'*ones(1,n);
V = x(2,:)'*ones(1,n);
dist = sqrt( (U-U').^2 + (V-V').^2 );
M = 1./(1+dist.^2);
a = (M\f')';

Für die angegebenen Daten liefert das Programm 


x=[0.6415    0.6628    0.3459    0.1000    0.8296    0.8571    0.9000    0.6889 ;
   0.1000    0.4383    0.1791    0.3360    0.2237    0.5105    0.3075    0.9000 ];

f=[ 418   260   443   394   348   469   242   292 ];

pos=[0.5182;0.2567];

a=landscape(x,f);

distV=(pos(1)-x(1,:)).^2+(pos(2)-x(2,:)).^2;
sum(a./(1+distV))

einen Höhe von 278m für Vaihingen.

[Aufgabe]
  automatisch erstellt am 16. 11. 2007