
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 1545: Programm zur Approximation der Fourier-Koeffizienten |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
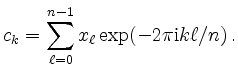
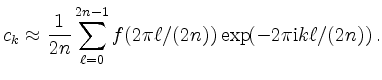
Diese kann in zwei Teilsummen aufgeteilt werden
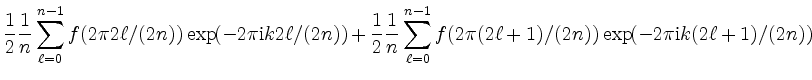 |
|||
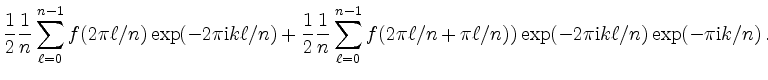 |
Der erste Summand ist 1/2 mal die Riemansumme für die halbe
Intervallzahl, der zweite ist 1/2 mal die Riemann-Summe für die
Intervall-Mittelpunkte bei der halben Intervallzahl mit dem Faktor
![]() korrigiert.
korrigiert.
Unter Vermeidung von doppelten Funktionsauswertung ergibt sich also die Funktion
function [c, steps] = fourier_coefficients(fct,k,tol)
% function c = f_coef(fct,k,tol)
% Fourier coefficients c_0, ..., c_k-1 of fct
% error <= tol, steps: number of refinements
MAX_STEPS = 8;
n = nextpow2(k); % for oiptimal fft
x = [0:n-1]*2*pi/n;
% initial Riemann sum
c = fft(feval(fct,x))/n;
c = c(1:k); % n >= k; only first k coefficients are relevant
for steps = 1:MAX_STEPS
% Riemann sum at interval mid-points
d = fft(feval(fct,x+pi/n))/n;
% combine Riemann sums as in FFT-recursion
d = d(1:k) .* exp(-pi*i*[0:k-1]/n);
c = (c+d)/2;
% check tolerance: c-c_old = c - (2c -d) = d-c
if max(abs(d-c))<tol;
return;
end;
% refinement, double points
n = 2*n;
x = [0:n-1]*2*pi/n;
end;
| automatisch erstellt am 27. 11. 2007 |