Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1566: Genauigkeit von Gauß-Formeln und Romberg-Verfahren

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Vergleichen Sie die Genauigkeit der Gauß-Legendre-Formeln und des Romberg-Algorithmus für die Berechnung des Integrals

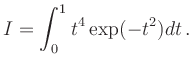
$\displaystyle I= \int_0^1 t^4 \exp(-t^2) dt \,. $

Bestimmen Sie dazu für $ 2,3,5,9,17$ Funktionsauswertungen jeweils die Fehler zum exakten Wert

$\displaystyle I= 0.10026879814501736705519586439\ldots $

Es können die zum Download bereitgestellten Programme romberg und gauss_par verwendet werden. Das Programm romberg ist so anzupassen, dass es eine feste Anzahl von Schritten durchführt.

Dies führt zu dem Programm 


function gauss_romberg_vergleich
n=[2,3,5,9,17];

exakt=0.1002687981450173670551958643;
%exakt=pi/4;
fct=@(t)t.^4./exp(t.^2);
%fct=@(t)1./(1+t.^2);

r=romberg(fct,0,1,2,4);

[t,w]=gauss_par(n(end));

for k=1:length(n)
  g(k)=w{n(k)}'*fct(t{n(k)});
end

romberg_fehler=(r-exakt)'/exakt

gauss_fehler=(g-exakt)'/exakt


function R = romberg(F,a,b,n,steps)
h = (b-a)/(n-1); 

% erste Trapezsumme, Spaltenvektor der Dimension von F
x = [a:h:b+h/2];
Fx = feval(F,x); 
Fx(:,1) = Fx(:,1)/2; 
Fx(:,n) = Fx(:,n)/2;
S = sum(Fx')'*h; R = S;

% Extrapolation
for j=1:steps;
   % j-te Trapezsumme
   x = [a+h/2:h:b];
   Fx = feval(F,x);
   % letze Tableau-Zeile, ergaenzt um Trapezsumme
   S = [(S(:,1)+h*sum(Fx')')/2 S];
   % Ueberscheiben mit neuer Tableau-Zeile
   for k=1:j;
      S(:,k+1) = (4^k*S(:,k) - S(:,k+1))/(4^k-1);
   end;
   h = h/2; R = [R,S(:,j+1)];
   % Fehlerschaetzung 
end;

Der Aufruf liefert das Ergebnis: 


romberg_fehler =

   0.83446619475474       
   0.0648808546841555       
   0.00238720276595473     
  -2.60836878188279e-05      
   7.86458571202453e-08


gauss_fehler =

   4.527738397988407e-02
  -2.373373589393931e-03
  -1.718648312397936e-06
  -3.307899713000076e-14
  -1.384058457322208e-16
[Aufgabe]
  automatisch erstellt am 10.  1. 2008