
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Interaktive Aufgabe 1166: Maximaler Geradenabstand bei linearer Kongruenzmethode |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
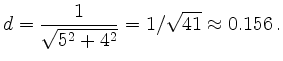
Dass es keinen ganzzahligen Vektor mit kleinerer Norm gibt bei dem das
Skalarprodukt mod ![]() verschwindet, kann man
leicht nachrechnen.
verschwindet, kann man
leicht nachrechnen.
Das Programm
a=71;b=a;v=a/359; % Startwerte
for k=2:358 % Berechnen der Vektoren
b=mod(b*a,359);
v=[v,b/359];
end
plot(v(1:2:357),v(2:2:358),'ok') % Plot der 2d-Vektoren
hold on
N=[4,5];d=1/norm(N); % Normalenrichtung und Abstand der Geradenschar
anz=sum(abs(N))-1; % Maximale Anzahl paralleler Geraden in [0,1]^2
N=sign(N(1))*N*d; % Normierung des Normalenvektors
for k=1:anz % Geraden haben höchstens Länge sqrt(2)
plot([k*N(1)*d-sqrt(2)*N(2),k*N(1)*d+sqrt(2)*N(2)],...
[k*N(2)*d+sqrt(2)*N(1),k*N(2)*d-sqrt(2)*N(1)],'-k');
end
axis([0,1,0,1]); % Einschränkung auf [0,1]^2
erzeugt das Bild
![\includegraphics[width=6cm]{g8_1_l.eps}](/inhalt/loesung/loesung989/img6.png)
| automatisch erstellt am 10. 1. 2008 |