
Mathematik-Online:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online: | |
Geometrie |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Sei der zugrundegelegte Körper
![]() oder
oder
![]() . Sei
. Sei ![]() .
.
Orthogonalität.
Seien
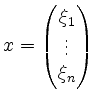 und
und
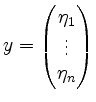 Vektoren im
Vektoren im ![]() .
.
Sei
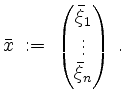
Ist
![]() , so ist
, so ist ![]() .
.
Das Skalarprodukt von ![]() und
und ![]() ist gegeben durch
ist gegeben durch
Die Länge (oder auch Norm) von ![]() ist gegeben durch
ist gegeben durch
Der Vektor ![]() heißt normiert, falls
heißt normiert, falls ![]() .
.
Ist ![]() , so schreiben wir
, so schreiben wir
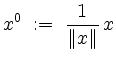
für den normierten Vektor von
Die Cauchy-Schwarzsche Ungleichung schreibt sich nun
Sind ![]() und
und ![]() , und ist
, und ist ![]() der von
der von ![]() und
und ![]() eingeschlossene Winkel, so gilt
eingeschlossene Winkel, so gilt
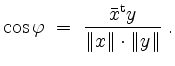
Die Vektoren ![]() und
und ![]() heißen orthogonal, falls
heißen orthogonal, falls
![]() .
Im Falle
.
Im Falle ![]() und
und ![]() ist dies gleichbedeutend damit, daß der von
ist dies gleichbedeutend damit, daß der von ![]() und
und ![]() eingeschlossene Winkel gleich
eingeschlossene Winkel gleich
![]() ist.
ist.
Ein Tupel
![]() von Vektoren in
von Vektoren in ![]() heißt orthonormal, falls
heißt orthonormal, falls ![]() und
und ![]() orthogonal sind
für alle
orthogonal sind
für alle
![]() mit
mit ![]() , und
, und ![]() normiert ist für alle
normiert ist für alle
![]() .
.
Ein orthonormales Tupel ist insbesondere linear unabhängig. Es ist dann eine Orthonormalbasis von
![]() .
.
Die orthogonale Projektion von ![]() auf
auf ![]() ist gegeben durch
ist gegeben durch
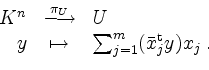
Der Abstand eines Punktes ![]() zum Unterraum
zum Unterraum ![]() ist gegeben durch
ist gegeben durch
![]() .
.
Der von dem Vektor ![]() und dem Unterraum
und dem Unterraum ![]() eingeschlossene Winkel ist gleich dem von den Vektoren
eingeschlossene Winkel ist gleich dem von den Vektoren ![]() und
und ![]() eingeschlossenen Winkel, falls
eingeschlossenen Winkel, falls
![]() . Falls
. Falls
![]() , so ist dieser Winkel gleich
, so ist dieser Winkel gleich ![]() - es steht
- es steht ![]() orthogonal zu
orthogonal zu ![]() genau dann, wenn seine orthogonale
Projektion auf
genau dann, wenn seine orthogonale
Projektion auf ![]() verschwindet.
verschwindet.
Gram-Schmidtsches Orthonormalisierungsverfahren.
Seien
![]() gegeben.
gegeben.
Das folgende Verfahren liefert eine Orthonormalbasis von
![]() .
.
Setze
![]() .
.
Sind
![]() bereits konstruiert für ein
bereits konstruiert für ein ![]() , so setze man
, so setze man
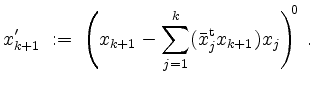
Die Normierung werde nur dann durchgeführt, wenn der zu normierende Vektor ![]() ist. Ansonsten überspringe man
den Vektor
ist. Ansonsten überspringe man
den Vektor ![]() und fahre mit
und fahre mit ![]() an seiner statt fort. Denn dann hat man
an seiner statt fort. Denn dann hat man
![]() nachgewiesen,
und
nachgewiesen,
und ![]() war als Erzeuger von
war als Erzeuger von ![]() redundant.
redundant.
Als Resultat ist
![]() eine Orthonormalbasis von
eine Orthonormalbasis von
![]() . Es gilt
. Es gilt ![]() genau
dann, wenn
genau
dann, wenn
![]() linear unabhängig ist.
linear unabhängig ist.
Kreuzprodukt.
Seien
 und
und
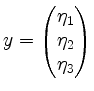 Vektoren im
Vektoren im
![]() .
.
Das Kreuzprodukt von ![]() und
und ![]() ist definiert als
ist definiert als
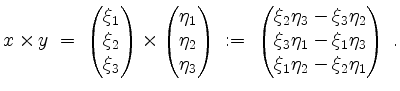
Der Vektor ![]() ist orthogonal zu
ist orthogonal zu ![]() und zu
und zu ![]() . Seine Länge ist gleich dem Flächeninhalt des von
. Seine Länge ist gleich dem Flächeninhalt des von ![]() und
und ![]() aufgespannten Parallelogramms. Insbesondere ist
aufgespannten Parallelogramms. Insbesondere ist
![]() genau dann, wenn
genau dann, wenn ![]() linear abhängig ist.
linear abhängig ist.
Die Richtung von ![]() kann man sich wie folgt veranschaulichen. Man wähle ein Koordinatensystem,
in dem die
kann man sich wie folgt veranschaulichen. Man wähle ein Koordinatensystem,
in dem die ![]() -Achse in Richtung des Daumens der rechten Hand, die
-Achse in Richtung des Daumens der rechten Hand, die ![]() -Achse in Richtung des
Zeigefingers und die
-Achse in Richtung des
Zeigefingers und die ![]() -Achse in Richtung des Mittelfingers zeigt. Legt man nun den Daumen der rechten Hand
in Richtung des Vektors
-Achse in Richtung des Mittelfingers zeigt. Legt man nun den Daumen der rechten Hand
in Richtung des Vektors ![]() und den Zeigefinger in Richtung des Vektors
und den Zeigefinger in Richtung des Vektors ![]() , so zeigt der Mittelfinger in
Richtung des Kreuzproduktes
, so zeigt der Mittelfinger in
Richtung des Kreuzproduktes ![]() .
.
Es gelten folgende Regeln. Seien
![]() , und seien
, und seien
![]() .
.
Hessesche Normalenform.
Sei
![]() ein Unterraum der Dimension
ein Unterraum der Dimension ![]() , mit
, mit
![]() , und sei
, und sei
![]() . Wir wollen
. Wir wollen
mit einer geeigneten Matrix
Sei hierzu
![]() eine Basis von
eine Basis von ![]() , welche wir zu einer Basis
, welche wir zu einer Basis
![]() von
von ![]() ergänzen.
Gram-Schmidt auf diese Basis angewandt liefert eine Orthonormalbasis
ergänzen.
Gram-Schmidt auf diese Basis angewandt liefert eine Orthonormalbasis
![]() derart,
daß
derart,
daß
![]() eine Basis von
eine Basis von ![]() darstellt. Sei nun
darstellt. Sei nun
![]() die Matrix mit Zeilentupel
die Matrix mit Zeilentupel
![]() . Mit
. Mit ![]() wird
wird
Die Darstellung von
Der Abstand
![]() eines Punktes
eines Punktes ![]() zu
zu ![]() ist dann gegeben durch
ist dann gegeben durch
![]() .
.
Beispiele:
| automatisch erstellt am 11. 8. 2006 |