
Mathematik-Online:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online: | |
Determinanten |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Permutationen.
Sei
![]() . Eine Permutation von
. Eine Permutation von
![]() ist eine bijektive Abbildung
ist eine bijektive Abbildung
![]() . Wir schreiben sie als
. Wir schreiben sie als
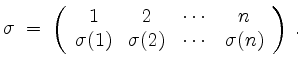
Die identische Abbildung, die alle Zahlen in
![]() festläßt, wird mit
festläßt, wird mit
![]() oder
kurz mit
oder
kurz mit
![]() bezeichnet.
bezeichnet.
Die Menge aller Permutationen von
![]() wird mit
wird mit
![]() bezeichnet. Sie enthält
bezeichnet. Sie enthält ![]() Elemente.
Elemente.
Zum Beispiel ist
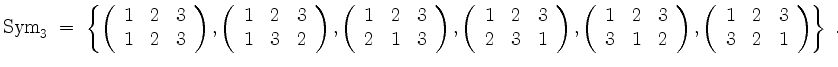
Zykelschreibweise.
Ein Zykel wird geschrieben als
mit paarweise verschiedenen
Zum Beispiel ist, in der Reihenfolge wie oben,
Jede Permutation
![]() kann als Produkt paarweise disjunkter Zykel geschrieben werden.
Zwei Zykel heißen hierbei disjunkt, falls sie kein gemeinsames Element aufweisen. Um diese
Zykelschreibweise zu erhalten, verfahre man etwa wie folgt.
kann als Produkt paarweise disjunkter Zykel geschrieben werden.
Zwei Zykel heißen hierbei disjunkt, falls sie kein gemeinsames Element aufweisen. Um diese
Zykelschreibweise zu erhalten, verfahre man etwa wie folgt.
Sei ![]() . Der erste Zykel ist gegeben durch
. Der erste Zykel ist gegeben durch
wobei
Sei
![]() minimal unter den Zahlen, die nicht im ersten Zykel auftreten.
Der zweite Zykel ist gegeben durch
minimal unter den Zahlen, die nicht im ersten Zykel auftreten.
Der zweite Zykel ist gegeben durch
wobei
Sei
![]() minimal unter den Zahlen, die nicht in den ersten beiden Zykeln auftreten.
Der dritte Zykel ist gegeben durch
minimal unter den Zahlen, die nicht in den ersten beiden Zykeln auftreten.
Der dritte Zykel ist gegeben durch
wobei
Und so fort, bis nach dem ![]() -ten Schritt alle Zahlen in
-ten Schritt alle Zahlen in
![]() abgehandelt sind. Wir erhalten
abgehandelt sind. Wir erhalten
Da die Kompositionsreihenfolge wegen Disjunktheit der Zykel keine Rolle spielt, wird das Verknüpfungszeichen
Zykel der Länge
So wird zum Beispiel
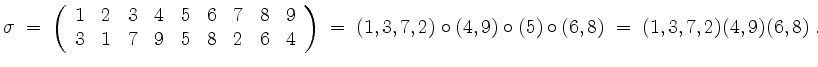
Signum.
Das Signum oder Vorzeichen einer Permutation
ist gegeben durch
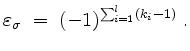
In anderen Worten, ein Zykel gerader Länge hat negatives Vorzeichen, ein Zykel ungerader Länge hat positives Vorzeichen, und zur Bestimmung des Vorzeichens einer Permutation multipliziere man die Vorzeichen ihrer Zykel.
Es ist
für
Definition der Determinante.
Sei ![]() ein Körper, sei
ein Körper, sei ![]() , und sei
, und sei
![]() . Sei die Determinante
von
. Sei die Determinante
von ![]() definiert durch die Leibnizsche Formel
definiert durch die Leibnizsche Formel
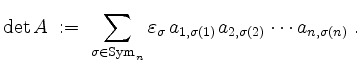
Zum Beispiel ist für
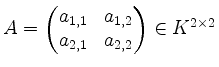 mit
mit
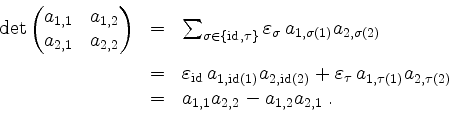
Regeln.
Seien
![]() . Dann ist
. Dann ist
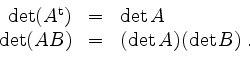
Die Determinante einer oberen Blockdreiecksmatrix berechnet sich zu
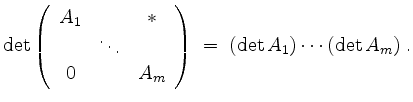
Dabei seien
Beachte insbesondere, daß für eine ![]() -Matrix
-Matrix
![]() gilt, daß
gilt, daß
Laplace-Entwicklung.
Sei
Für
die Matrix, welche aus
Die Determinante von ![]() läßt sich durch die Laplace-Entwicklung nach der
läßt sich durch die Laplace-Entwicklung nach der ![]() -ten Zeile
-ten Zeile
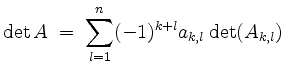
oder nach der
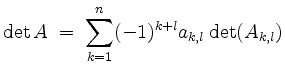
berechnen.
Gaußschritte.
Gaußsche Umformungen können verwendet werden, um eine Matrix
![]() zwecks
Determinantenberechnung zu vereinfachen.
zwecks
Determinantenberechnung zu vereinfachen.
Dasselbe gilt für Spaltenumformungen.
In der Praxis verwendet man häufig Gaußschritte zur Vorbereitung einer Laplace-Entwicklung durch weitgehendes Säubern einer Zeile oder einer Spalte.
Regularität, Cramer.
Sei
![]() . Die Matrix
. Die Matrix ![]() ist genau dann invertierbar, wenn
ist genau dann invertierbar, wenn
![]() .
.
Genauer, es gilt dann die Cramersche Regel,
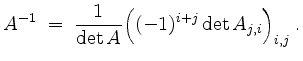
In der Praxis verwendet man diese Regel hauptsächlich zur Berechnung einzelner Einträge von ![]() .
.
Flächen- und Volumenberechnung.
Zwei Vektoren
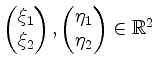 spannen ein Parallelogramm
spannen ein Parallelogramm
![$\displaystyle \{\lambda\begin{pmatrix}\xi_1 \\ \xi_2\end{pmatrix}+\mu\begin{pmatrix}\eta_1 \\ \eta_2\end{pmatrix}\;\vert\; \lambda,\mu\in[0,1]\}
$](/inhalt/vstatisch/vstatisch53/img74.png)
auf. Sein Flächeninhalt ist gegeben durch
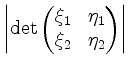 .
.
Drei Vektoren
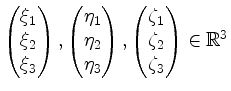 spannen ein Parallelotop
spannen ein Parallelotop
![$\displaystyle \{\lambda\begin{pmatrix}\xi_1\\ \xi_2\\ \xi_3\end{pmatrix}+\mu\be...
...ix}\zeta_1\\ \zeta_2\\ \zeta_3\end{pmatrix}\;\vert\; \lambda,\mu,\nu\in[0,1]\}
$](/inhalt/vstatisch/vstatisch53/img77.png)
auf. Sein Volumen ist gegeben durch
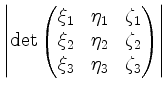 .
.
Allgemeiner, sei
![]() mit
mit ![]() . Das von den Spaltenvektoren von
. Das von den Spaltenvektoren von ![]() aufgespannte
aufgespannte ![]() -Parallelotop
-Parallelotop
![$\displaystyle \{A\cdot\begin{pmatrix}\lambda_1\\ \vdots\\ \lambda_k\end{pmatrix}\;\vert\; \lambda_1,\ldots,\lambda_k\in[0,1]\}\subseteq\mathbb{R}^n
$](/inhalt/vstatisch/vstatisch53/img81.png)
hat das
Ist speziell ![]() und
und ![]() , so ist dieses Volumen gleich
, so ist dieses Volumen gleich
![]() , wobei
, wobei
![]() mit
mit
![]() sei.
sei.
Beispiele:
| automatisch erstellt am 11. 8. 2006 |