
Mathematik-Online:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online: | |
Differenzierbarkeit |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Offene Mengen.
Es sei ![]() und
und
![]() gegeben. Ein Punkt
gegeben. Ein Punkt ![]() heißt innerer Punkt von
heißt innerer Punkt von ![]() , falls es ein
, falls es ein
![]() gibt, so
daß
gibt, so
daß
![]() .
.
Die Menge ![]() heißt offen, wenn jeder Punkt
heißt offen, wenn jeder Punkt ![]() innerer Punkt von
innerer Punkt von ![]() ist.
ist.
Die Menge ![]() ist genau dann offen, wenn ihr Komplement
ist genau dann offen, wenn ihr Komplement
![]() abgeschlossen ist.
abgeschlossen ist.
Partielle Ableitung.
Sei
![]() . Gegeben seien
. Gegeben seien
![]() und ein Punkt
und ein Punkt
![]() .
Die Funktion
.
Die Funktion ![]() heißt partiell differenzierbar nach
heißt partiell differenzierbar nach ![]() in
in ![]() , falls
, falls
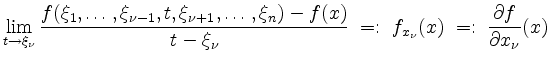
existiert. In diesem Falle heißt der Grenzwert
differenzierbar in
Gegeben seien nun
![]() mit den Komponenten
mit den Komponenten
![]() und ein innerer Punkt
und ein innerer Punkt
![]() .
Die Funktion
.
Die Funktion ![]() heißt partiell differenzierbar nach
heißt partiell differenzierbar nach ![]() in
in ![]() , falls die Funktionen
, falls die Funktionen
![]() jeweils partiell differenzierbar nach
jeweils partiell differenzierbar nach ![]() in
in ![]() sind. In diesem Falle heißt der Vektor
sind. In diesem Falle heißt der Vektor
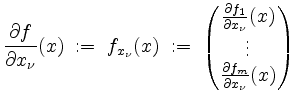
die partielle Ableitung von
Die Funktion ![]() heißt partiell differenzierbar in
heißt partiell differenzierbar in ![]() , wenn
, wenn ![]() partiell differenzierbar nach
partiell differenzierbar nach ![]() in
in ![]() ist für alle
ist für alle
![]() . Im Falle
. Im Falle ![]() heißt dann der Vektor
heißt dann der Vektor
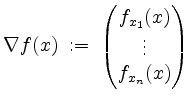
der Gradient von
Die Funktion
![]() heißt partiell differenzierbar, wenn
heißt partiell differenzierbar, wenn ![]() partiell differenzierbar in allen
Punkten
partiell differenzierbar in allen
Punkten ![]() ist.
ist.
Die Funktion ![]() heißt stetig partiell differenzierbar, wenn
heißt stetig partiell differenzierbar, wenn ![]() partiell differenzierbar ist und die
partielle Ableitung
partiell differenzierbar ist und die
partielle Ableitung
![]() stetig ist für alle
stetig ist für alle
![]() und alle
und alle
![]() .
.
Seien nun
![]() gegeben. Dann definiert man rekursiv die
gegeben. Dann definiert man rekursiv die
![]() -fache partielle Ableitung von
-fache partielle Ableitung von ![]() nach
nach
![]() in
in ![]() durch
durch
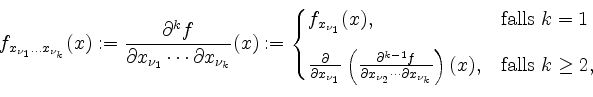
falls die rechte Seite existiert.
Sei ![]() . Die Funktion
. Die Funktion
![]() heißt
heißt ![]() -fach stetig differenzierbar, in Zeichen
-fach stetig differenzierbar, in Zeichen
![]() , falls
alle
, falls
alle ![]() -fachen partiellen Ableitungen von
-fachen partiellen Ableitungen von ![]() in allen Punkten
in allen Punkten ![]() existieren und stetig sind.
existieren und stetig sind.
Richtungsableitung.
Sei
![]() , sei
, sei
![]() eine Funktion, und sei
eine Funktion, und sei ![]() ein innerer Punkt.
Sei
ein innerer Punkt.
Sei ![]() eine Richtung im
eine Richtung im
![]() , d.h. sei
, d.h. sei
![]() und
und ![]() .
.
Die Funktion ![]() heißt differenzierbar in Richtung
heißt differenzierbar in Richtung ![]() in
in ![]() , falls
, falls
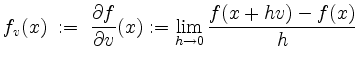
existiert. Der Wert
Ist speziell ![]() der
der ![]() -te Einheitsvektor in
-te Einheitsvektor in
![]() , so gilt
, so gilt
![]() ,
d.h. die Richtungsableitung in Richtung des
,
d.h. die Richtungsableitung in Richtung des ![]() -ten Einheitsvektors ist gleich der partiellen Ableitung nach
-ten Einheitsvektors ist gleich der partiellen Ableitung nach ![]() .
.
(Totale) Ableitung.
Sei
![]() , sei
, sei
![]() eine Funktion, und sei
eine Funktion, und sei ![]() ein innerer Punkt.
ein innerer Punkt.
Die Funktion ![]() heißt (total) differenzierbar in
heißt (total) differenzierbar in ![]() , falls es eine Matrix
, falls es eine Matrix
![]() und
eine Funktion
und
eine Funktion
![]() gibt, so daß
gibt, so daß
für alle
Falls
![]() offen ist, so heißt die Funktion
offen ist, so heißt die Funktion ![]() (total) differenzierbar, falls sie
in jedem Punkt
(total) differenzierbar, falls sie
in jedem Punkt ![]() differenzierbar ist. (Man setzt ,,total``
manchmal zur Betonung des Unterschiedes zur partiellen Differenzierbarkeit
hinzu.)
differenzierbar ist. (Man setzt ,,total``
manchmal zur Betonung des Unterschiedes zur partiellen Differenzierbarkeit
hinzu.)
Ist ![]() differenzierbar in
differenzierbar in ![]() , so ist die obengenannte Matrix
, so ist die obengenannte Matrix ![]() eindeutig bestimmt und heißt die
(totale) Ableitung von
eindeutig bestimmt und heißt die
(totale) Ableitung von ![]() in
in ![]() , manchmal auch Jacobimatrix von
, manchmal auch Jacobimatrix von ![]() in
in ![]() , und wir schreiben
, und wir schreiben
Es gilt dann
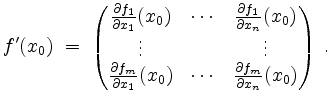
Zum Beispiel ist im Falle ![]() die Jacobimatrix mit dem Gradienten über die Gleichung
die Jacobimatrix mit dem Gradienten über die Gleichung
![]() verbunden. (Hier hat man also
zwei Begriffe für bis auf Transposition dieselbe Matrix. Dafür gibt es einen Grund, wie wir weiter unten bei den Vektorfeldern
sehen werden.)
verbunden. (Hier hat man also
zwei Begriffe für bis auf Transposition dieselbe Matrix. Dafür gibt es einen Grund, wie wir weiter unten bei den Vektorfeldern
sehen werden.)
Ist
![]() differenzierbar in
differenzierbar in ![]() , so existieren auch alle Richtungsableitungen von
, so existieren auch alle Richtungsableitungen von ![]() in
in ![]() . Für
jede Richtung
. Für
jede Richtung ![]() in
in
![]() gilt dann
gilt dann
Ist ![]() differenzierbar in
differenzierbar in ![]() , so ist
, so ist ![]() insbesondere partiell differenzierbar in
insbesondere partiell differenzierbar in ![]() .
.
Ist
![]() offen und
offen und
![]() stetig partiell differenzierbar, so ist
stetig partiell differenzierbar, so ist ![]() differenzierbar.
differenzierbar.
Ist
![]() offen, so gelten folgende Implikationen für eine Funktion
offen, so gelten folgende Implikationen für eine Funktion
![]() .
.

Regeln für (totale) Ableitungen.
Sei
![]() , und sei
, und sei ![]() ein innerer Punkt.
ein innerer Punkt.
Es seien
![]() und
und
![]() differenzierbar im inneren Punkt
differenzierbar im inneren Punkt ![]() , und es seien
, und es seien
![]() . Dann sind auch
. Dann sind auch
![]() ,
,
![]() ,
, ![]() in
in ![]() differenzierbar, und
es gelten die Differentiationsregeln
differenzierbar, und
es gelten die Differentiationsregeln
Sei ferner
![]() , sei
, sei ![]() in einem inneren Punkt
in einem inneren Punkt ![]() differenzierbar, und sei
differenzierbar, und sei
![]() differenzierbar
im inneren Punkt
differenzierbar
im inneren Punkt ![]() . Wir haben also
. Wir haben also
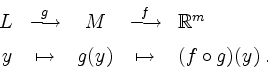
Dann ist
Die Hessematrix.
Sei
![]() offen, und sei
offen, und sei
![]() eine zweifach stetig differenzierbare Funktion.
eine zweifach stetig differenzierbare Funktion.
Die Hessematrix von ![]() in
in ![]() ist durch
ist durch
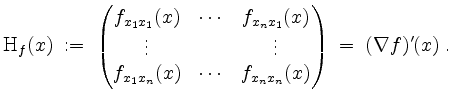
definiert.
Der Satz von Schwarz besagt, daß unter diesen Voraussetzungen
![]() für alle
für alle
![]() gilt,
d.h. daß die Hessematrix
gilt,
d.h. daß die Hessematrix
![]() symmetrisch ist für alle
symmetrisch ist für alle ![]() .
.
| automatisch erstellt am 11. 8. 2006 |