
Mathematik-Online:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online: | |
Kurvenintegrale und konservative Vektorfelder |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Kurven.
Sei ![]() . Eine Kurve im
. Eine Kurve im
![]() ist eine stetige Abbildung
ist eine stetige Abbildung
![]() für gewisse
für gewisse
![]() mit
mit ![]() . Man nennt
. Man nennt
![]() den Anfangspunkt und
den Anfangspunkt und ![]() den Endpunkt der Kurve
den Endpunkt der Kurve ![]() . Eine Kurve, deren
Anfangspunkt gleich ihrem Endpunkt ist, heißt geschlossene Kurve.
. Eine Kurve, deren
Anfangspunkt gleich ihrem Endpunkt ist, heißt geschlossene Kurve.
Der Träger einer Kurve ![]() ist
definiert als
ist
definiert als
Falls
Ist die Funktion
![]() differenzierbar, so heißt
differenzierbar, so heißt
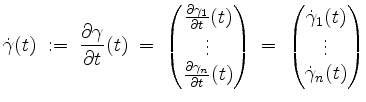
der Tangentialvektor von
Die Kurve ![]() heißt stückweise stetig differenzierbar, falls es so eine Unterteilung
heißt stückweise stetig differenzierbar, falls es so eine Unterteilung
![]() gibt, daß
gibt, daß
![]() stetig differenzierbar ist für
stetig differenzierbar ist für
![]() . Eine stückweise stetig
differenzierbare Kurve nennt man auch Weg.
. Eine stückweise stetig
differenzierbare Kurve nennt man auch Weg.
Die Länge eines solchen Weges
![]() ist gegeben durch
ist gegeben durch
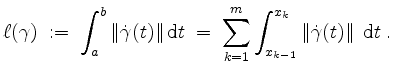
Kurvenintegrale.
Sei
![]() ein Weg und
ein Weg und
![]() eine stetige Funktion. Dann ist das
Kurvenintegral von
eine stetige Funktion. Dann ist das
Kurvenintegral von ![]() längs
längs ![]() gegeben durch
gegeben durch
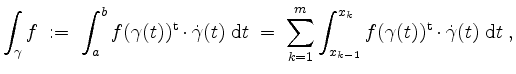
wobei
Schreibt man
![]() und
und
![]() , so sei auch
folgende Schreibweise erlaubt.
, so sei auch
folgende Schreibweise erlaubt.
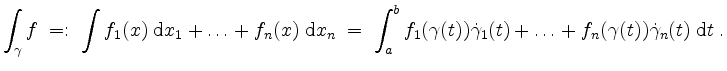
Zum Beispiel sei
Äquivalenz von Kurven.
Zwei Wege
![]() und
und
![]() heißen äquivalent, falls es eine bijektive, streng
monoton wachsende Funktion
heißen äquivalent, falls es eine bijektive, streng
monoton wachsende Funktion
![]() so gibt, daß
so gibt, daß
![]() . D.h. es ist
. D.h. es ist
![]() für alle
für alle
![]() .
.
Sind ![]() und
und ![]() äquivalente Wege im
äquivalente Wege im
![]() , so sind
, so sind
für alle stetigen Funktionen
Grob gesagt, die Länge eines Weges und das Kurvenintegral längs eines Weges hängt nur vom Träger der Kurve und dem
Durchlaufsinn ab. Daher kann man eine Kurve auch als Menge im
![]() zusammen mit einem Durchlaufsinn betrachten. Eine
zugehörige Abbildung
zusammen mit einem Durchlaufsinn betrachten. Eine
zugehörige Abbildung
![]() heißt dann eine Parameterdarstellung der Kurve, und alle möglichen
Parameterdarstellungen sind zueinander äquivalent.
heißt dann eine Parameterdarstellung der Kurve, und alle möglichen
Parameterdarstellungen sind zueinander äquivalent.
Einfacher Zusammenhang und Sterngebiete.
Sei
![]() ein Gebiet, d.h. eine offene und zusammenhängende Teilmenge.
ein Gebiet, d.h. eine offene und zusammenhängende Teilmenge.
Das Gebiet ![]() heißt einfach zusammenhängend, falls sich jeder geschlossene Weg
heißt einfach zusammenhängend, falls sich jeder geschlossene Weg
![]() stetig in einen Punkt
zusammenziehen läßt, ohne
stetig in einen Punkt
zusammenziehen läßt, ohne ![]() zu verlassen. Formal besagt diese Forderung, es gebe für jedes solche
zu verlassen. Formal besagt diese Forderung, es gebe für jedes solche ![]() eine stetige Funktion
eine stetige Funktion
![]() mit
mit
![]() und
und
![]() konstant, wobei
konstant, wobei
![]() ,
,
![]() .
.
Ein Gebiet
![]() in der Ebene ist einfach zusammenhängend genau dann, wenn es, anschaulich gesprochen, ,,keine Löcher hat``.
in der Ebene ist einfach zusammenhängend genau dann, wenn es, anschaulich gesprochen, ,,keine Löcher hat``.
Zum Beispiel ist die punktierte Ebene
![]() nicht einfach zusammenhängend.
nicht einfach zusammenhängend.
Dieses anschauliche Kriterium läßt sich nicht direkt auf mehr Dimensionen verallgemeinern. Zum Beispiel ist der punktierte
Raum
![]() einfach zusammenhängend.
einfach zusammenhängend.
Ein Gebiet
![]() heißt sternförmig, falls es ein Zentrum
heißt sternförmig, falls es ein Zentrum ![]() gibt so, daß für alle
gibt so, daß für alle ![]() die Verbindungsstrecke
die Verbindungsstrecke
![]() in
in ![]() enthalten ist.
enthalten ist.
Zum Beispiel ist jedes konvexe Gebiet sternförmig. Andererseits ist ist die geschlitzte Ebene
![]() sternförmig mit Zentrum
sternförmig mit Zentrum
![]() , aber nicht konvex.
, aber nicht konvex.
Jedes sternförmige Gebiet ist einfach zusammenhängend.
Andererseits ist die Menge
einfach zusammenhängend, aber nicht sternförmig, wie man der Skizze entnimmt.
![\includegraphics[width = 8cm]{r.eps}](/inhalt/vstatisch/vstatisch61/img56.png)
Konservative Vektorfelder.
Sei
![]() ein Gebiet. Sei
ein Gebiet. Sei
![]() eine Funktion. Man nennt
eine Funktion. Man nennt ![]() dann auch ein Vektorfeld.
dann auch ein Vektorfeld.
Eine Stammfunktion von ![]() ist eine differenzierbare Funktion
ist eine differenzierbare Funktion
![]() so, daß
so, daß
![]() , d.h.
, d.h.
![]() .
Falls eine Stammfunktion
.
Falls eine Stammfunktion ![]() von
von ![]() existiert, so spricht man bei
existiert, so spricht man bei ![]() auch von einem konservativen Vektorfeld
(oder einem Gradientenfeld).
auch von einem konservativen Vektorfeld
(oder einem Gradientenfeld).
Für ein Vektorfeld
![]() sind folgende Aussagen äquivalent:
sind folgende Aussagen äquivalent:
Der erste Hauptsatz für Kurvenintegrale besagt folgendes.
Ist das Vektorfeld
![]() konservativ, und ist
konservativ, und ist
![]() eine
Stammfunktion von
eine
Stammfunktion von ![]() , so gilt für jeden Weg
, so gilt für jeden Weg
![]()
Ist ![]() ein geschlossener Weg und
ein geschlossener Weg und ![]() ein konservatives Vektorfeld, so gilt also
ein konservatives Vektorfeld, so gilt also
![]() .
.
Integrabilitätsbedingungen.
Sei
![]() ein Gebiet. Sei
ein Gebiet. Sei
![]() ein Vektorfeld.
ein Vektorfeld.
Wir sagen, ![]() erfüllt die Integrabilitätsbedingungen, falls
erfüllt die Integrabilitätsbedingungen, falls ![]() stetig differenzierbar ist und
stetig differenzierbar ist und
auf
Ein stetig differenzierbares konservatives Vektorfeld erfüllt stets die Integrabilitätsbedingungen, wie man mit Hilfe des Satzes von Schwarz sieht.
Der zweite Hauptsatz für Kurvenintegrale besagt folgendes.
Ist
![]() ein stetig differenzierbares Vektorfeld auf einem einfach zusammenhängenden Gebiet
ein stetig differenzierbares Vektorfeld auf einem einfach zusammenhängenden Gebiet ![]() , so ist
, so ist ![]() konservativ genau dann,
wenn
konservativ genau dann,
wenn ![]() die Integrabilitätsbedingungen erfüllt.
die Integrabilitätsbedingungen erfüllt.
Beispiele:
| automatisch erstellt am 11. 8. 2006 |