Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online:

Integralsätze

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Divergenz und Rotation.
Es seien $ M\subseteq \mathbb{R}^n$ offen, $ f=(f_1,\ldots,f_n)^\mathrm{t} :M\to\mathbb{R}^n$ ein Vektorfeld auf $ M$ und $ \Phi:M\to\mathbb{R}$ eine skalare Funktion auf $ M$ . Wir definieren, falls existent,

(i)
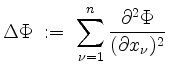$ \Delta\Phi \;:=\; \displaystyle\sum\limits_{\nu=1}^n\dfrac{\partial^2\Phi}{(\partial x_\nu)^2}$     (Laplace $ \Phi$ )
(ii)
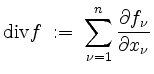$ \mathrm{div }f \;:=\; \displaystyle\sum\limits_{\nu=1}^n\dfrac{\partial f_\nu}{\partial x_\nu}$     (Divergenz $ f$ )
(iii)
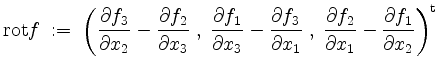$ \mathrm{rot }f \;:=\; \left(\dfrac{\partial f_3}{\partial x_2}-\dfrac{\partial... ...partial f_2}{\partial x_1}-\dfrac{\partial f_1}{\partial x_2}\right)^\mathrm{t}$ (Rotation $ f$ ), falls $ n=3$ .

Eine Merkregel zur Rotation ist der formale Ausdruck

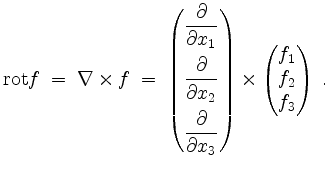
$\displaystyle \mathrm{rot }f \; =\; \nabla\times f \;=\; \begin{pmatrix}\dfrac{... ...partial x_3}\end{pmatrix}\times \begin{pmatrix}f_1\\ f_2\\ f_3\end{pmatrix}\;. $

Der Greensche Integralsatz.

Eine nichtleere Menge $ K\subseteq \mathbb{R}^2$ heißt regulär, falls

(i)
$ K$ kompakt und zusammenhängend ist, und
(ii)
der Rand $ \partial K$ gleich dem Träger eines geschlossenen Weges $ \gamma: [a,b]\to\mathbb{R}^2$ ist, der abgesehen von seinem Anfangs- und Endpunkt doppelpunktfrei ist.

Wir schreiben dann in suggestiver Weise $ \partial K$ anstelle von $ \gamma$ . Wir erinnern daran, daß ein Weg eine stückweise stetig differenzierbare Kurve ist.

Wir setzen dabei stets voraus, daß $ K$ links zur Durchlaufrichtung der Kurve $ \gamma$ aus (ii) liegt. Man spricht hierbei vom positiv orientierten Rand von $ K$ . Es seien ferner $ O\subseteq\mathbb{R}^2$ eine offene Obermenge von $ K$ und $ f:O\to\mathbb{R}^2$ ein stetig differenzierbares Vektorfeld.

Der Greensche Integralsatz besagt, daß

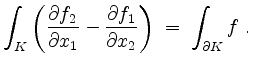
$\displaystyle \int_K\left(\frac{\partial f_2}{\partial x_1}-\frac{\partial f_1}{\partial x_2}\right) \;=\; \int_{\partial K}f\ . $

Wendet man den Greeenschen Integralsatz auf $ f(x_1,x_2):=\frac{1}{2}(-x_2,x_1)^\mathrm{t}$ an, so gilt insbesondere die folgende Formel für den Flächeninhalt von $ K$ .

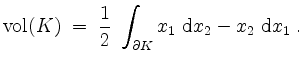
$\displaystyle \mathrm{vol}(K) \;=\; \dfrac{1}{2}\;\int_{\partial K} x_1\;\mathrm{d}x_2-x_2\;\mathrm{d}x_1\;. $

Der Stokessche Integralsatz.

Sei $ K\subseteq \mathbb{R}^2$ regulär, mit $ \partial K$ parametrisiert von $ \gamma: [a,b]\to\mathbb{R}^2$ . Sei $ \Phi:K \to \mathbb{R}^3$ eine Fläche. Ferner existiere eine offene Obermenge $ O\supseteq K$ derart, daß sich $ \Phi$ fortsetzen läßt zu einer zweimal stetig differenzierbaren Funktion $ \tilde\Phi:O\to\mathbb{R}^3$ . Es bezeichne $ \partial K$ den positiv orientieren Rand von $ K$ . Dann sei $ \partial \Phi :=\Phi(\partial K) = \Phi\circ(\partial K)$ der entsprechende positiv orientierte Rand der Fläche von $ \Phi$ .

Sei $ G\supseteq \mathcal T(\Phi)$ eine offene Obermenge des Trägers von $ \Phi$ , und sei $ f:G\to\mathbb{R}^3$ ein stetig differenzierbares Vektorfeld.

Der Stokessche Integralsatz besagt, daß

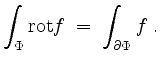
$\displaystyle \int_\Phi\mathrm{rot }f \;=\; \int_{\partial\Phi}f\;. $

Der Gaußsche Integralsatz.

Eine Fläche $ \Phi:K \to \mathbb{R}^3$ heißt regulär, falls

(i)
$ K\subseteq \mathbb{R}^2$ regulär ist,
(ii)
$ \Phi$ injektiv auf dem Inneren von $ K$ ist, und
(iii)
der Normalenvektor $ \mathrm{n}_\Phi:=\Phi_{x_1}\times\Phi_{x_2}$ auf dem Inneren von $ K$ nicht verschwindet.

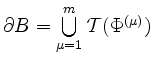Es sei $ B \subseteq \mathbb{R}^3$ kompakt und zusammenhängend, und dergestalt, daß $ \partial B=\bigcup\limits_{\mu=1}^m \mathcal{T}(\Phi^{(\mu)})$ eine endliche Vereinigung von regulären Flächen $ \Phi^{(1)},\ldots,\Phi^{(m)}$ ist,

Kurz, sei $ \partial B$ stückweise stetig differenzierbar mit nach außen weisendem Normalenvektor und sich annullierenden Rändern der Flächenstücke parametrisiert. Man spricht dann bei $ \partial B$ auch von einer orientierbaren Fläche.

Sei $ G\subseteq\mathbb{R}^3$ eine offene Obermenge von $ B$ . Sei $ f:G\to\mathbb{R}^3$ ein stetig differenzierbares Vektorfeld.

Dann besagt der Gaußsche Integralsatz, daß

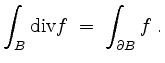
$\displaystyle \int_B \mathrm{div }f \;=\; \int_{\partial B} f\;. $

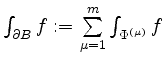Dabei sei $ \partial B$ als suggestive Schreibweise für die Summe aller Flächen $ \Phi^{(1)},\ldots,\Phi^{(m)}$ aufgefaßt, d.h. $ \int_{\partial B} f:=\sum\limits_{\mu=1}^m\int_{\Phi^{(\mu)}} f$ .

(Autoren: Künzer/Martin/Tentler/Wahrheit)
[Beispiele] [Verweise]
  automatisch erstellt am 11.  8. 2006