
Mathematik-Online:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online: | |
Fourierentwicklung |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Periodische Funktionen.
Eine Funktion
![]() heißt periodisch
mit Periode
heißt periodisch
mit Periode ![]() , falls sie auf ganz
, falls sie auf ganz
![]() die Identität
die Identität
erfüllt. Die einfachsten periodischen Funktionen sind
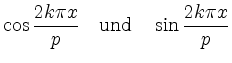
sowie
für
![]() -Linearkombinationen periodischer Funktionen sind periodisch.
-Linearkombinationen periodischer Funktionen sind periodisch.
Trigonometrische Polynome.
Eine Funktion
![]() der Gestalt
der Gestalt
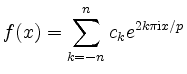
mit
Setzt man für ![]()
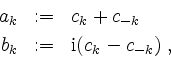
so ist
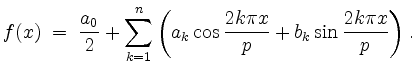
Umgekehrt erhält man für ![]() aus den Koeffizienten
aus den Koeffizienten ![]() und
und ![]() die Koeffizienten
die Koeffizienten ![]() durch
durch
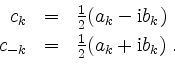
zurück.
Beachte, daß alle Koeffizienten ![]() ,
, ![]() genau dann reell sind, wenn stets
genau dann reell sind, wenn stets
![]() gilt.
gilt.
Trigonometrische Reihen
Eine trigonometrische Reihe mit Periode ![]() ist eine Funktionenreihe der Gestalt
ist eine Funktionenreihe der Gestalt
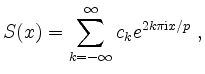
mit
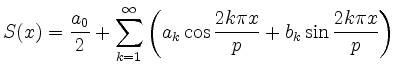
geschrieben werden kann.
Eine trigonometrische Reihe kann konvergieren oder divergieren.
Fourierkoeffizienten und Fourierreihen.
Es sei ![]() und
und
![]() eine
eine ![]() -periodische, über
-periodische, über ![]() integrierbare Funktion. Die Fourierkoeffizienten von
integrierbare Funktion. Die Fourierkoeffizienten von
![]() sind folgendermaßen gegeben.
sind folgendermaßen gegeben.
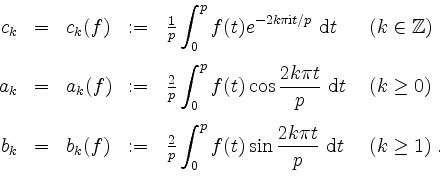
Wegen der
Dann hängen die Koeffizienten ![]() ,
, ![]() und
und ![]() wie oben beschrieben zusammen.
wie oben beschrieben zusammen.
Ist die Funktion ![]() auf
auf
![]() eine bis auf endlich viele Ausnahmestellen gerade Funktion, oder allgemeiner, ist dort fast überall
eine bis auf endlich viele Ausnahmestellen gerade Funktion, oder allgemeiner, ist dort fast überall
![]() , so gilt
, so gilt
![]() für alle
für alle ![]() .
.
Ist die Funktion ![]() auf
auf
![]() eine bis auf endlich viele Ausnahmestellen ungerade Funktion, oder allgemeiner, ist dort fast überall
eine bis auf endlich viele Ausnahmestellen ungerade Funktion, oder allgemeiner, ist dort fast überall
![]() , so gilt
, so gilt
![]() für alle
für alle ![]() .
.
Die Fourierreihe oder Fourierentwicklung von ![]() ist gegeben durch
ist gegeben durch
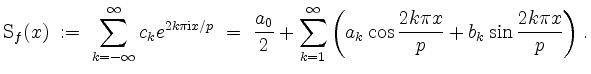
Konvergenz von Fourierreihen.
Sei
![]()
![]() -periodisch und integrierbar über
-periodisch und integrierbar über ![]() . Gilt für
. Gilt für
![]() , daß dort
, daß dort
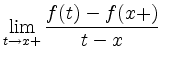 und
und
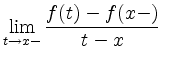 existieren (d.h. einseitige Ableitungen
existieren),
existieren (d.h. einseitige Ableitungen
existieren),
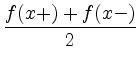 .
.
Anschaulich gesprochen, hat ![]() bei
bei ![]() eine Tangente von links und eine Tangente von rechts, so ist der Wert der Fourierreihe bei
eine Tangente von links und eine Tangente von rechts, so ist der Wert der Fourierreihe bei ![]() genau der Mittelwert des links- und rechtsseitigen Funktionswertes von
genau der Mittelwert des links- und rechtsseitigen Funktionswertes von ![]() an dieser Stelle.
an dieser Stelle.
Insbesondere, ist ![]() bei
bei ![]() differenzierbar, so ist
differenzierbar, so ist
![]() . Das ist der Regelfall.
. Das ist der Regelfall.
Allgemeiner, auch wenn ![]() bei
bei ![]() stetig und links- wie rechtsseitig differenzierbar ist, so gilt dort
stetig und links- wie rechtsseitig differenzierbar ist, so gilt dort
![]() .
.
Anschaulich, hat ![]() bei
bei ![]() einen Knick, aber sowohl links- wie rechtsseitig eine Tangente, so hat die Fourierreihe dort trotzdem den selben Funktionswert wie
einen Knick, aber sowohl links- wie rechtsseitig eine Tangente, so hat die Fourierreihe dort trotzdem den selben Funktionswert wie ![]() .
.
Der reelle Fall.
Ist ![]() wie oben, nur reellwertig, so ist stets
wie oben, nur reellwertig, so ist stets
![]() , und folglich
, und folglich
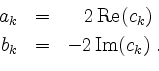
Summandenweises Ableiten.
Es sei
![]()
![]() -periodisch, auf
-periodisch, auf ![]() stetig differenzierbar bis auf endlich viele Ausnahmestellen und
an diesen Ausnahmestellen noch stetig.
stetig differenzierbar bis auf endlich viele Ausnahmestellen und
an diesen Ausnahmestellen noch stetig.
Sei ![]() die
die ![]() -periodische Funktion, die außer an den Ausnahmestellen die Ableitung von
-periodische Funktion, die außer an den Ausnahmestellen die Ableitung von ![]() darstellt, und die an einer Ausnahmestelle
darstellt, und die an einer Ausnahmestelle ![]() den
Wert
den
Wert
![]() annimmt, so erhalten wir durch summandenweises Differenzieren
annimmt, so erhalten wir durch summandenweises Differenzieren
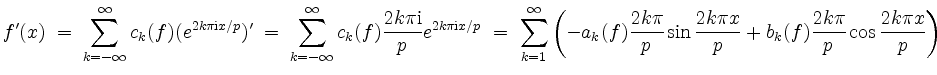
für alle
Kennt man umgekehrt die Fourierreihe zu ![]() und möchte auf die Fourierreihe von
und möchte auf die Fourierreihe von ![]() schließen, wobei
schließen, wobei ![]() die ebengenannten Bedingungen erfüllt,
so genügt es,
die ebengenannten Bedingungen erfüllt,
so genügt es, ![]() zu berechnen.
zu berechnen.
Beispiele:
| automatisch erstellt am 11. 8. 2006 |