
Mathematik-Online:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online: | |
Die Matrixexponentialfunktion |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Definition.
Es sei ![]() und
und
![]() . Wir definieren
. Wir definieren
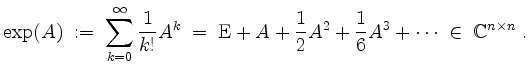
Diese Reihe konvergiert eintragsweise für alle
Eigenschaften.
Sind
![]() , und ist
, und ist ![]() , so ist
, so ist
![]() .
.
Ist
![]() , und ist
, und ist
![]() invertierbar, so ist
invertierbar, so ist
![]() .
.
Sind
![]() für
für
![]() , und für gewisse
, und für gewisse ![]() , so ist
, so ist
d.h.
In der Regel stellt sich die Frage nach der Berechnung von ![]() mit
mit
![]() und einem Parameter
und einem Parameter
![]() .
.
Einsetzen von Jordanblöcken.
Seien ![]() und
und
![]() gegeben. Wir erinnern an die Bezeichnungsweise
gegeben. Wir erinnern an die Bezeichnungsweise
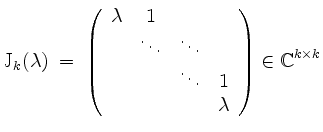
für einen Jordanblock der Kantenlänge
Für
![]() wird nun
wird nun
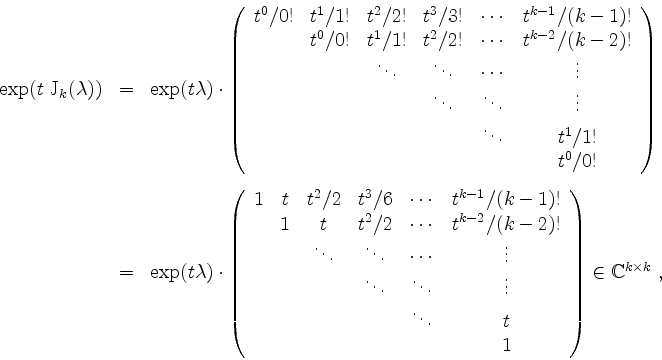
wobei
Berechnung von ![]() allgemein.
allgemein.
Sei
![]() . Berechne die Jordanform von
. Berechne die Jordanform von ![]() in der Form
in der Form
mit
Mit obigen Regeln folgt
worin man nun die oben angegebene Formel für
Entsprechend ergibt sich ![]() im Spezialfall
im Spezialfall ![]() , sollte das einmal gefragt sein.
, sollte das einmal gefragt sein.
| automatisch erstellt am 11. 8. 2006 |