
Mathematik-Online-Kurs: Repetitorium HM II - Mehrdimensionale Analysis

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Kurs: Repetitorium HM II - Mehrdimensionale Analysis | |
Integralsätze |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
Divergenz und Rotation.
Es seien
![]() offen,
offen,
![]() ein Vektorfeld auf
ein Vektorfeld auf ![]() und
und
![]() eine skalare Funktion auf
eine skalare Funktion auf ![]() . Wir definieren, falls existent,
. Wir definieren, falls existent,
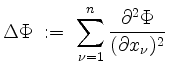 (Laplace
(Laplace 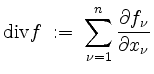 (Divergenz
(Divergenz 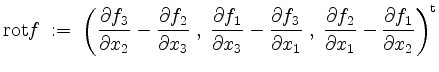 (Rotation
(Rotation Eine Merkregel zur Rotation ist der formale Ausdruck
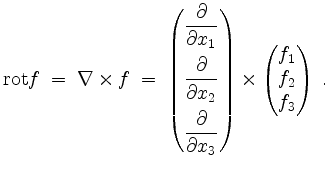
Der Greensche Integralsatz.
Eine nichtleere Menge
![]() heißt regulär, falls
heißt regulär, falls
Wir schreiben dann in suggestiver Weise
![]() anstelle von
anstelle von ![]() .
Wir erinnern daran, daß ein Weg eine stückweise stetig differenzierbare Kurve ist.
.
Wir erinnern daran, daß ein Weg eine stückweise stetig differenzierbare Kurve ist.
Wir setzen dabei stets voraus, daß ![]() links zur Durchlaufrichtung der Kurve
links zur Durchlaufrichtung der Kurve ![]() aus (ii) liegt.
Man spricht hierbei vom positiv orientierten Rand von
aus (ii) liegt.
Man spricht hierbei vom positiv orientierten Rand von ![]() .
Es seien ferner
.
Es seien ferner
![]() eine offene Obermenge von
eine offene Obermenge von ![]() und
und
![]() ein stetig differenzierbares Vektorfeld.
ein stetig differenzierbares Vektorfeld.
Der Greensche Integralsatz besagt, daß
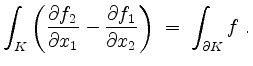
Wendet man den Greeenschen Integralsatz auf
![]() an, so gilt insbesondere
die folgende Formel für den Flächeninhalt von
an, so gilt insbesondere
die folgende Formel für den Flächeninhalt von ![]() .
.
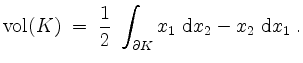
Der Stokessche Integralsatz.
Sei
![]() regulär, mit
regulär, mit
![]() parametrisiert von
parametrisiert von
![]() . Sei
. Sei
![]() eine Fläche.
Ferner existiere eine offene Obermenge
eine Fläche.
Ferner existiere eine offene Obermenge
![]() derart, daß sich
derart, daß sich ![]() fortsetzen läßt zu einer zweimal
stetig differenzierbaren Funktion
fortsetzen läßt zu einer zweimal
stetig differenzierbaren Funktion
![]() . Es bezeichne
. Es bezeichne
![]() den positiv orientieren Rand
von
den positiv orientieren Rand
von ![]() . Dann sei
. Dann sei
![]() der
entsprechende positiv orientierte Rand der Fläche von
der
entsprechende positiv orientierte Rand der Fläche von ![]() .
.
Sei
![]() eine offene Obermenge des Trägers von
eine offene Obermenge des Trägers von ![]() , und sei
, und sei
![]() ein stetig differenzierbares Vektorfeld.
ein stetig differenzierbares Vektorfeld.
Der Stokessche Integralsatz besagt, daß
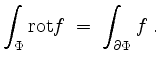
Der Gaußsche Integralsatz.
Eine Fläche
![]() heißt regulär, falls
heißt regulär, falls
Es sei
![]() kompakt und zusammenhängend, und dergestalt, daß
kompakt und zusammenhängend, und dergestalt, daß
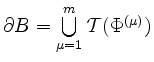 eine endliche Vereinigung von regulären Flächen
eine endliche Vereinigung von regulären Flächen
![]() ist,
ist,
Kurz, sei
![]() stückweise stetig differenzierbar mit nach außen weisendem Normalenvektor und sich annullierenden Rändern der Flächenstücke parametrisiert.
Man spricht dann bei
stückweise stetig differenzierbar mit nach außen weisendem Normalenvektor und sich annullierenden Rändern der Flächenstücke parametrisiert.
Man spricht dann bei
![]() auch von einer orientierbaren Fläche.
auch von einer orientierbaren Fläche.
Sei
![]() eine offene Obermenge von
eine offene Obermenge von ![]() . Sei
. Sei
![]() ein stetig differenzierbares Vektorfeld.
ein stetig differenzierbares Vektorfeld.
Dann besagt der Gaußsche Integralsatz, daß
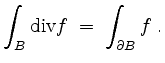
Dabei sei
![]() als suggestive Schreibweise für die Summe aller Flächen
als suggestive Schreibweise für die Summe aller Flächen
![]() aufgefaßt, d.h.
aufgefaßt, d.h.
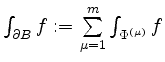 .
.
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 16.2.2011 |