
Mathematik-Online-Kurs: Repetitorium HM II - Fourieranalysis

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Kurs: Repetitorium HM II - Fourieranalysis | |
Parsevalsche Gleichungen |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
Es sei ![]() und
und
![]() zwei
zwei ![]() -periodische Funktionen, für die in
-periodische Funktionen, für die in ![]() nur endlich viele Unstetigkeitsstellen
liegen, und für die in jeder solchen Unstetigkeitsstelle der links- und der rechtsseitige Grenzwert existieren.
nur endlich viele Unstetigkeitsstellen
liegen, und für die in jeder solchen Unstetigkeitsstelle der links- und der rechtsseitige Grenzwert existieren.
Dann gilt die Parsevalsche Skalarproduktgleichung
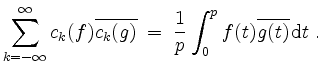
Insbesondere gilt die Parsevalsche Normgleichung
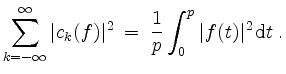
Speziell kann eine Folge
![]() nur als Koeffizientenfolge einer Fourierreihe einer wie eingangs beschriebenen Funktion auftreten, wenn
die Quadratsumme
nur als Koeffizientenfolge einer Fourierreihe einer wie eingangs beschriebenen Funktion auftreten, wenn
die Quadratsumme
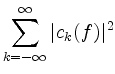 konvergiert.
konvergiert.
Darüberhinaus liefert jede Fourierentwicklung als ,,Nebenprodukt``noch den Wert von
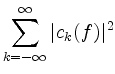 . Manchmal ist dies
unser einziger Weg zur Auswertung der entstandenen Reihe. Z.B. wird sich
. Manchmal ist dies
unser einziger Weg zur Auswertung der entstandenen Reihe. Z.B. wird sich
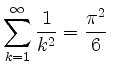 ergeben.
ergeben.
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 16.2.2011 |