Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Repetitorium HM II - Differentialgleichungssysteme

Systeme linearer Differentialgleichungen mit konstanten Koeffizienten

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Differentialgleichungen vom Typ $ \dot y = A y$ . Homogene lineare Systeme mit konstanten Koeffizienten.

Es sei $ A\in\mathbb{C}^{n\times n}\,$ , $ n\geq 1i\,$ . Wir suchen die vektorwertigen differenzierbaren Funktionen $ \mathbb{R}\to\mathbb{C}^n$ , $ t\mapsto y(t)$ , die der Differentialgleichung

$\displaystyle \dot y(t) \;=\; A y(t) $

für alle $ t\in\mathbb{R}$ genügen. Oft schreibt man für diese Gleichung auch kurz

$\displaystyle \dot y \;=\; A y\; . $

Die Lösungsgesamtheit $ \mathrm{L}(A,0)$ dieser Differentialgleichung bildet einen $ n$ -dimensionalen Vektorraum über $ \mathbb{C}$ . Es ist $ \frac{\mathrm{d}}{\mathrm{d}t} \exp(tA) = A\exp(tA)$ , und daher genügt jede Spalte von $ \exp(tA)$ dieser Differentialgleichung. Da das Tupel der Spalten von $ \exp(tA)$ ferner linear unabhängig ist, bilden diese Spalten eine $ \mathbb{C}$ -lineare Basis des Lösungsraums.

Eine Matrix $ F(t)$ , deren Einträge von $ t$ abhängen, und deren Spalten eine $ \mathbb{C}$ -lineare Basis von $ \mathrm{L}(A,0)$ bilden, nennt man Fundamentalmatrix dieser Differentialgleichung. So ist z.B. $ \exp(tA)$ eine Fundamentalmatrix von $ \dot y(t) = A y(t)$ . Jede Lösung dieser Differentialgleichung läßt sich dann eindeutig in der Form $ F(t) v$ für ein $ v\in\mathbb{C}^n$ darstellen.

In der Praxis berechnet man nun eine Matrix $ J$ in Jordanform mit

$\displaystyle S^{-1}AS \;=\; J\;. $

Dann bildet die Matrix

$\displaystyle \exp(tA)S \;=\; S\exp(tJ) $

genau wie $ \exp(tA)$ eine Fundamentalmatrix. Es ist also nicht nötig, die Matrix $ S^{-1}$ zu berechnen, um zu einer Fundamentalmatrix zu kommen.

Differentialgleichungen vom Typ $ \dot y = A y + b$ . Inhomogene lineare Systeme mit konstanten Koeffizienten.

Sei nun zusätzlich eine differenzierbare Funktion $ b:\mathbb{R}\to\mathbb{C}^n$ gegeben. Die Lösungsgesamtheit $ \mathrm{L}(A,b)$ der Differentialgleichung

$\displaystyle \dot y(t) \;=\; A y(t) + b(t) $

ist gegeben durch

$\displaystyle \mathrm{L}(A,b) = y_\mathrm{p} + \mathrm{L}(A,0), $

wobei $ y_\mathrm{p}$ eine spezielle (partikuläre) Lösung des inhomogenen Systems und $ \mathrm{L}(A,0)$ die Lösungsgesamtheit des zugehörigen homogenen Systems ist.

Sämtliche Lösungen sind also von der Form

$\displaystyle y(t) \; =\; y_\mathrm{p}(t) + y_\mathrm{h}(t) \; , $

wobei $ y_\mathrm{p}$ eine partikuläre Lösung des inhomogenen Systems, $ y_\mathrm{h}$ eine beliebige Lösung des zugehörigen homogenen Systems ist.

Um eine partikuläre Lösung zu finden, verwendet man die Methode der Variation der Konstanten. Diese sieht den Ansatz $ y_\mathrm{p}(t) = F(t)v(t)$ mit einer Fundamentalmatrix $ F$ des zugehörigen homogenen Systems vor.

Differenziert man diesen Ausdruck, so erhält man

$\displaystyle y_\mathrm{p}'(t)\; =\; F'(t)v(t)+F(t)v'(t)\; =\; Ay_\mathrm{p}(t)+F(t)v'(t)\; . $

Ist

$\displaystyle v'(t)\; =\; F(t)^{-1} b(t) $

(Matrixinversion), so ist $ y_\mathrm{p}$ eine Lösung des inhomogenen Systems.

Man hat also mit

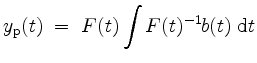
$\displaystyle y_\mathrm{p}(t) \; =\; F(t) \int F(t)^{-1} b(t) \; \mathrm{d}t $

eine partikuläre Lösung des inhomogenen Systems gefunden.

Verwendet man speziell die Fundamentalmatrix $ F(t)=\exp(tA)$ , so ist $ F(t)^{-1}=\exp(-tA)$ . Verwendet man hingegen die Fundamentalmatrix $ F(t)=S\exp(tJ)$ , so ist $ F(t)^{-1}=\exp(-tJ)S^{-1}$ .

Homogene lineare Differentialgleichungen $ n$ -ter Ordnung mit konstanten Koeffizienten.

Die Lösungsgesamtheit aller $ n$ -mal differenzierbaren Funktionen $ y$ , die der homogenen linearen Differentialgleichung $ n$ -ter Ordnung mit konstanten Koeffizienten

$\displaystyle y^{(n)}(t) + c_{n-1} y^{(n-1)}(t) + \cdots + c_1 y^{(1)}(t) + c_0 y^{(0)}(t) \;=\; 0 $

mit $ c_i\in\mathbb{C}, \, 0 \leq i \leq n-1$ , genügen, bildet einen $ n$ -dimensionalen Vektorraum über $ \mathbb{C}$ .

Wir konstruieren eine Basis dieses Vektorraumes wie folgt.

Es sei das zugehörige charakteristische Polynom

$\displaystyle \chi(X) \; =\; X^n + c_{n-1} X^{n-1} + \cdots + c_1 X + c_0 $

vollständig faktorisiert zu

$\displaystyle \chi(X) \; =\; (X-\lambda_1)^{m_1} \cdots (X-\lambda_r)^{m_r}\; , $

wobei $ \lambda_1, \ldots, \lambda_r \in \mathbb{C}$ paarweise verschieden sind.

Dann ist eine Basis dieser Lösungsgesamtheit gegeben durch

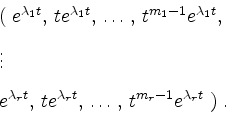
\begin{displaymath} \begin{array}{l} (\; e^{\lambda_1 t}, \, t e^{\lambda_1 t},... ...}, \, \ldots, \, t^{m_r-1} e^{\lambda_r t} \; )\; . \end{array}\end{displaymath}

Diese Basis ist im allgemeinen komplexwertig.

Sind alle $ c_i$ reell, und ist man an einer reellwertigen Basis der Lösungsgesamtheit interessiert, so geht man wie folgt vor. Es sei abermals das zugehörige charakteristische Polynom vollständig faktorisiert zu

$\displaystyle \chi(X) \; =\; (X-\lambda_1)^{m_1} \cdots (X-\lambda_r)^{m_r}\; , $

jedoch mit paarweise verschiedenen $ \lambda_1, \ldots, \lambda_l \in \mathbb{R}$ , $ \lambda_\nu = \alpha_\nu + \mathrm{i} \beta_\nu \in \mathbb{C} \setminus \mathbb{R}$ mit $ \alpha_\nu, \beta_\nu \in \mathbb{R}$ für $ l+1\le \nu\le r$ . Dabei seien die Nullstellen so geordnet, daß $ \operatorname{Im }\lambda_{l+1},\dots,\operatorname{Im }\lambda_s > 0$ und $ \operatorname{Im }\lambda_{s+1},\dots,\operatorname{Im }\lambda_r < 0$ . Dann ist eine reellwertige Basis der Lösungsgesamtheit gegeben durch

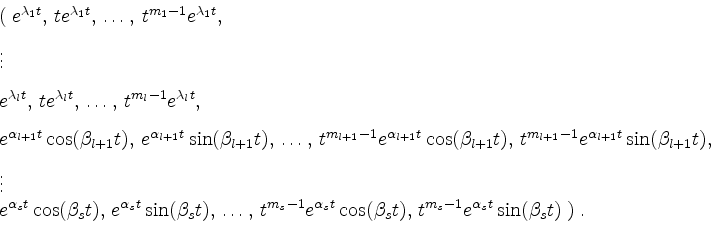
\begin{displaymath} \begin{array}{l} (\; e^{\lambda_1 t}, \, t e^{\lambda_1 t},... ..., t^{m_s -1} e^{\alpha_s t} \sin(\beta_s t)\; )\; . \end{array}\end{displaymath}

Reduktion auf ein System erster Ordnung.

Wir möchten den Zusammenhang der homogenen linearen Differentialgleichung $ n$ -ter Ordnung mit konstanten Koeffizienten mit homogenen linearen Systemen von Differentialgleichungen mit konstanten Koeffizienten nicht verschweigen.

Setzen wir

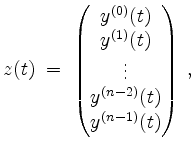
$\displaystyle z(t) \;=\; \begin{pmatrix} y^{(0)}(t) \\ y^{(1)}(t) \\ \vdots \\ y^{(n-2)}(t) \\ y^{(n-1)}(t) \\ \end{pmatrix}\; , $

so transformiert sich mit

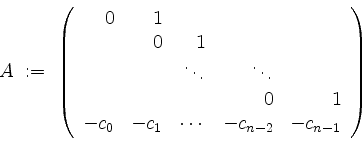
\begin{displaymath} A \; :=\; \left( \begin{array}{rrrrr} 0 & 1 & & & \\ & 0... ...0 & -c_1 & \cdots & -c_{n-2} & -c_{n-1} \\ \end{array}\right) \end{displaymath}

die lineare Differentialgleichung $ n$ -ter Ornung mit konstanten Koeffizienten in das homogene System mit konstanten Koeffizienten

$\displaystyle \dot z(t) \;=\; Az(t)\; . $

Das charakteristische Polynom der Matrix $ A$ entspricht dabei dem zugehörigen charakteristischen Polynom der gegebenen Differentialgleichung.

Analog kann man auch ein homogenes System $ n$ -ter Ordnung mit $ k$ abhängigen Variablen $ y_1$ , ..., $ y_k$ zurückführen auf ein homogenes System erster Ordnung mit $ n\cdot k$ abhängigen Variablen.

Inhomogene lineare Differentialgleichungen $ n$ -ter Ordnung mit konstanten Koeffizienten.

Die allgemeine Lösung der inhomogenen linearen Differentialgleichung $ n$ -ter Ordnung mit konstanten Koeffizienten

$\displaystyle y^{(n)}(t) + c_{n-1} y^{(n-1)}(t) + \cdots + c_1 y^{(1)}(t) + c_0 y^{(0)}(t) \;=\; g(t) $

mit $ c_i\in\mathbb{C}$ , $ 0 \leq i \leq n-1$ , und einer stetigen Funktion $ g:\mathbb{R}\to\mathbb{C}$ , $ t\mapsto g(t)$ , ist gegeben durch

$\displaystyle y(t) \; =\; y_\mathrm{p}(t) + y_\mathrm{h}(t) \; , $

wobei $ y_\mathrm{p}$ eine spezielle (partikuläre) Lösung der inhomogenen Differentialgleichung und $ y_\mathrm{h}$ die allgemeine Lösung der zugehörigen homogenen Differentialgleichung ist.

Nachdem im obigen Abschnitt beschrieben wird, wie man die allgemeine Lösung der homogenen Differentialgleichung erhält, möchten wir uns auf die Bestimmung einer partikulären Lösung $ y_\mathrm{p}$ konzentrieren. Dabei möchten wir drei Vorgehensweisen beschreiben.

I. Ansatz vom Typ der rechten Seite.

Oftmals besitzt die Funktion $ g$ , die in diesem Zusammenhang auch Störfunktion genannt wird, eine einfache Gestalt, für die sich der Lösungsansatz zur Bestimmung der partikulären Lösung gemäß der folgenden Tabelle ergibt.

\begin{displaymath} \begin{array}{\vert l\vert l\vert} \hline \mathrm{St''orfunk... ...''origen charakteristischen Polynoms ist}.\\ \hline \end{array}\end{displaymath}

Ist dabei $ \gamma $ bzw. $ \alpha + \mathrm{i} \beta$ keine Nullstelle des zugehörigen charakteristischen Polynoms, so wählen wir entsprechend $ \rho=0$ . Liegen ferner Linearkombinationen solcher Störfunktionen vor, so wählt man als Lösungsansatz für die partikuläre Lösung $ y_\mathrm{p}$ eine entsprechende Linearkombination der Ansatzfunktionen.

Man berechnet nun

$\displaystyle y_\mathrm{p}^{(n)}(t) + c_{n-1} y_\mathrm{p}^{(n-1)}(t) + \cdots + c_1 y_\mathrm{p}^{(1)}(t) + c_0 y_\mathrm{p}(t) $

und setzt dieses gleich der Störfunktion $ g(t)$ . Mittels Koeffizientenvergleich erhält man ein lineares Gleichungssystem, mit dem man schließlich die unbekannten Koeffizienten $ A_0, \ldots, A_m$ $ (\;, B_0, \ldots, B_m)$ bestimmt.

II. Variation der Konstanten

Wir wählen den folgenden Ansatz zur Bestimmung einer partikulären Lösung $ y_\mathrm{p}$ der gegebenen Differentialgleichung.

$\displaystyle y_\mathrm{p}(t) \; =\; c_1(t) y_1(t) + \cdots + c_n(t) y_n(t) \; , $

wobei die $ y_i$ linear unabhängige Lösungen der zugehörigen homogenen Differentialgleichung und die $ c_i$ noch zu bestimmende unbekannte Funktionen sind, $ 1 \leq i \leq n$ .

Die Funktionen $ c_i$ ermittelt man nun mittels der $ n$ Gleichungen

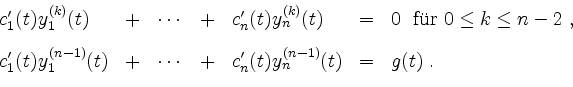
\begin{displaymath} \begin{array}{lccclcl} c_1'(t) y^{(k)}_1(t) & + & \cdots & +... ...ts & + & c_n'(t) y^{(n-1)}_n(t) & = & g(t) \; . \\ \end{array}\end{displaymath}

III. Zurückführung auf ein inhomogenes lineares System mit konstanten Koeffizienten.

Mit $ z(t)$ und $ A$ wie im homogenen Fall und mit

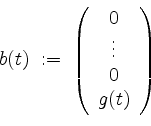
\begin{displaymath} b(t) \; :=\; \left( \begin{array}{c} 0 \\ \vdots \\ 0\\ g(t) \\ \end{array}\right) \end{displaymath}

transformiert sich die inhomogene lineare Differentialgleichung $ n$ -ter Ordnung mit konstanten Koeffizienten in das allgemeine System mit konstanten Koeffizienten

$\displaystyle \dot z(t) \;=\; Az(t) + b(t)\; . $

Der Lösungsansatz für dieses System wird oben beschrieben.
(Autoren: Künzer/Martin/Tentler/Wahrheit)

Beispiele

Aufgaben

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 16.2.2011