
Mathematik-Online-Kurs: Vektoranalysis - Potentialtheorie - Skalares Potential

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Kurs: Vektoranalysis - Potentialtheorie - Skalares Potential | |
Potential eines Gradientenfeldes |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
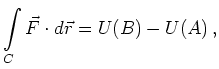
Insbesondere ist
![]() für
geschlossene Wege
für
geschlossene Wege ![]() .
.
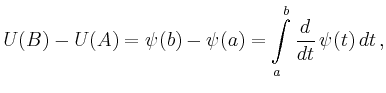
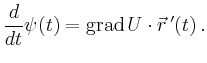
Wegen
![]() folgt
folgt
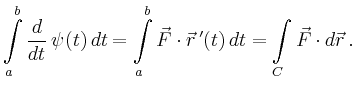
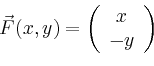
![$\displaystyle \vec{r}_1(t)=\left( \begin{array}{c} \cos t \\ \sin t\\ \end{array}\right),\quad t \in[0,\pi/2]\,,$](/inhalt/beispiel/beispiel708/img3.png) |
||
![$\displaystyle \vec{r}_2(t)=\left( \begin{array}{c} 1-t \\ 0\\ \end{array}\right),\quad t \in[0, 1]\,,$](/inhalt/beispiel/beispiel708/img5.png) |
||
![$\displaystyle \vec{r}_3(t)=\left( \begin{array}{c} 0\\ t\\ \end{array}\right),\quad t \in[0, 1]\,,$](/inhalt/beispiel/beispiel708/img7.png) |
![\includegraphics[width=.4\linewidth]{b_potential}](/inhalt/beispiel/beispiel708/img8.png)
Für das Arbeitsintegral von ![]() nach
nach ![]() entlang
entlang ![]() erhält man
erhält man
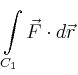 |
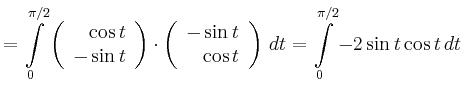 |
|
|
und entlang
| ||
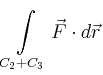 |
 |
|
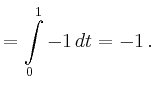 |
||
Verwendet man das Potential

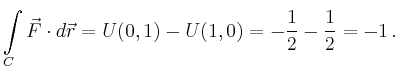
Beispielsweise ist für das Gravitationsfeld mit
![]() , d.h.
, d.h.
Um von einem Punkt ![]() aus das Gravitationsfeld zu
verlassen, muss damit die Arbeit
aus das Gravitationsfeld zu
verlassen, muss damit die Arbeit
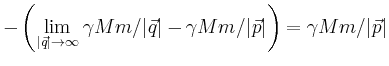
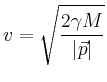
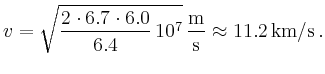
![\begin{displaymath}
C:\,\vec{r}(t)=\left(
\begin{array}{c}
\cos t \\ \sin t \\ ht/(2\pi)\\
\end{array}\right),\quad t\in[0,2\pi],
\end{displaymath}](/inhalt/beispiel/beispiel626/img2.png)
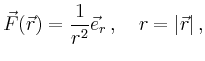
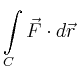 |
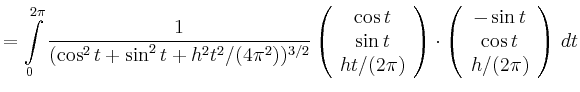 |
|
![$\displaystyle = \int\limits_0^{2\pi} \frac{h^2t/(4\pi^2)}{(1+h^2t^2/(4\pi^2))^{...
...frac{2\pi }{\sqrt{4\pi^2+h^2t^2}}\right]_0^{2\pi} = 1-\frac{1}{\sqrt{1+h^2}}\,.$](/inhalt/beispiel/beispiel626/img6.png) |
Alternativ lässt sich die Arbeit über die Differenz der Werte des Potentials
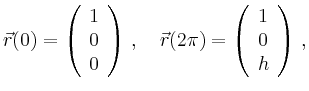
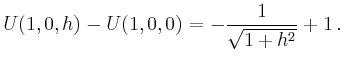
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 9.10.2013 |